23 luty 07 (57)

Następnie piszemy równanie prędkości punktu C, traktując ruch łącznika 2 jako ruch złożony, gdzie ruchem unoszenia jest ruch postępowy o prędkości liniowej v_B, natomiast ruchem względnym jest ruch obrotowy o środku obrotu w punkcie B, prędkość liniowa punktu v_CB wynika zatem z obrotowego ruchu względnego.

(v_c) = (vb) + (vcb)    ^_p22j

II AC 1AB    1BC

Analizujemy liczbę niewiadomych w równaniu (P2.2).

Pojedyncze podkreślenie oznacza że znany jest tylko kierunek wektora.

Podwójne podkreślenie oznacza że znany jest i kierunek i wartość wektora.

Taka analiza równania jest bardzo ważna ze względu na fakt, że rozwiązanie w układzie płaskim dowolnego równania wektorowego jest możliwe jedynie wtedy, gdy równanie to zawiera dokładnie dwie niewiadome (brak dwóch podkreśleń).

Kierunek prędkości względnej wynika z obrotu odcinka SC wokół punktu 6, natomiast kierunek prędkości punktu C należącego do łącznika 2 i do suwaka 3 wynika z konstrukcji mechanizmu. Suwak porusza się ruchem postępowym prostoliniowym.

Przyjmujemy punkt biegunowy n_v i rozwiązujemy wykreślnie w podziałce k_v równanie (P2.2), rysując tzw. plan prędkości (rys. 2.15).

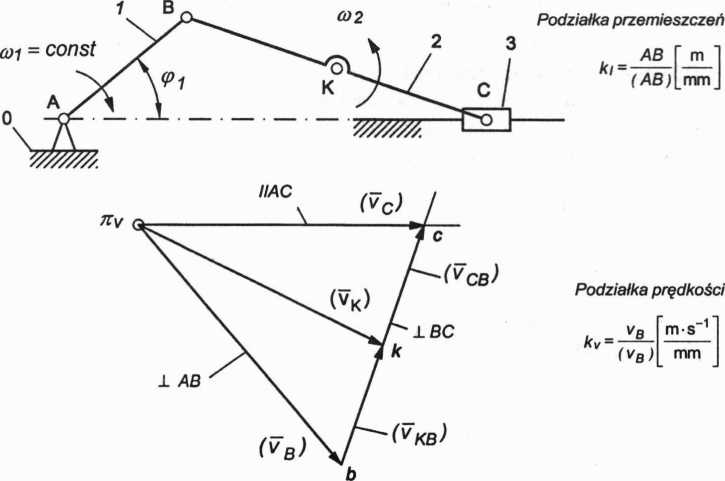
Rys. 2.15. Plan prędkości punktów mechanizmu korbowo-suwakowego

55