23 luty 07 (138)

Następnie w celu wykreślnego rozwiązania równania (P3.7) obliczamy wartości rysunkowe wszystkich znanych sił i zapisujemy równanie (P3.7) w postaci

( Rfy ) + ( Rl2 ) ⁺ ( &2 ) ⁺ ( ^2 ) ⁺ (&3 ) ⁺ ( G3 )+( P3 )+(Rq3) — 0    (P3.8)

Rysowanie wieloboku sił rozpoczynamy od pierwszej znanej całkowicie siły, w tym wypadku jest to siła (Rj₂), a kończymy na ostatniej znanej całkowicie sile, w tym wypadku jest to siła (P3 ), patrz rysunek 3.19b.

W celu zamknięcia wieloboku wektorowego opisanego równaniem (P3.7) rysujemy z początku wektora (f?/₂) kierunek reakcji (R?₂) a z końca wektora ostatniej znanej siły (P₃ ) kierunek reakcji (Rq₃ ). Te dwa kierunki zamykają wielobok sił dla grupy, pozwalając wyznaczyć nieznane wartości reakcji (R12) • (^03)■

Z wieloboku sił odczytujemy wartości rysunkowe (R12 ) = (P12 ) ⁺ (^12 ) oraz (Rq₃ ), a następnie obliczamy wartości: R₁₂ = (R12) • k_R1, R₀₃ = R₃₃ = (R₃₃ )-k_R1.

Na podstawie równania (P3.2) z planu sił odczytujemy reakcję (R₃₂), a na podstawie równania (P3.3) reakcję (R23)- Jak widać na planie sił (R23) ⁺ (^R32) = 0-

Wartość reakcji w punkcie C mechanizmu wynosi: R₂₃ =(R23)'^kRi-W ostatnim etapie należy przeprowadzić analizę sił działających na człon napędzający. Człon napędzający uwalniamy od więzów, przykładając siły zewnętrzne, wyznaczoną reakcję (R21) = -(R12), reakcję podstawy w punkcie A w postaci dwóch składowych stycznej (R^f01) i normalnej (R^) oraz moment równoważący M_r1. Uwalnianie od więzów członu napędzającego przedstawia rysunek 3.20a.

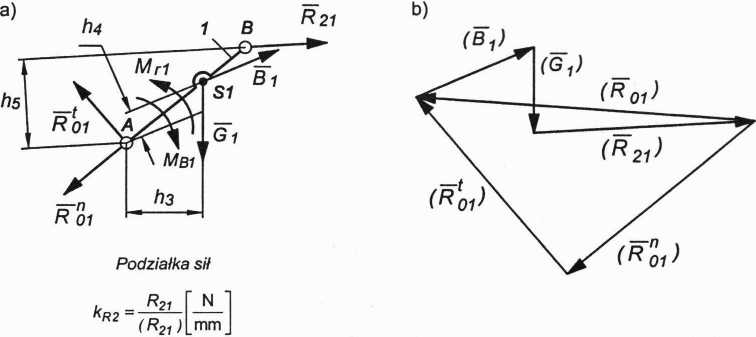
Rys. 3.20. Analiza sił działających na człon napędzający: a) uwalnianie od więzów członu napędzającego; b) plan sił członu napędzającego

137