23 luty 07 (146)

mi,Jsi B 2

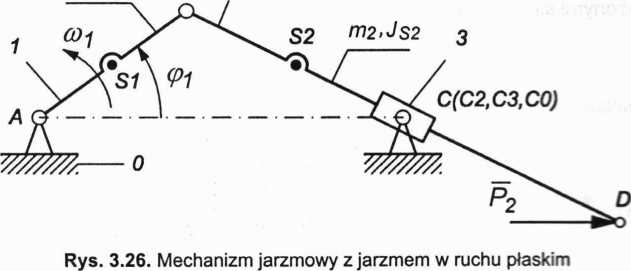
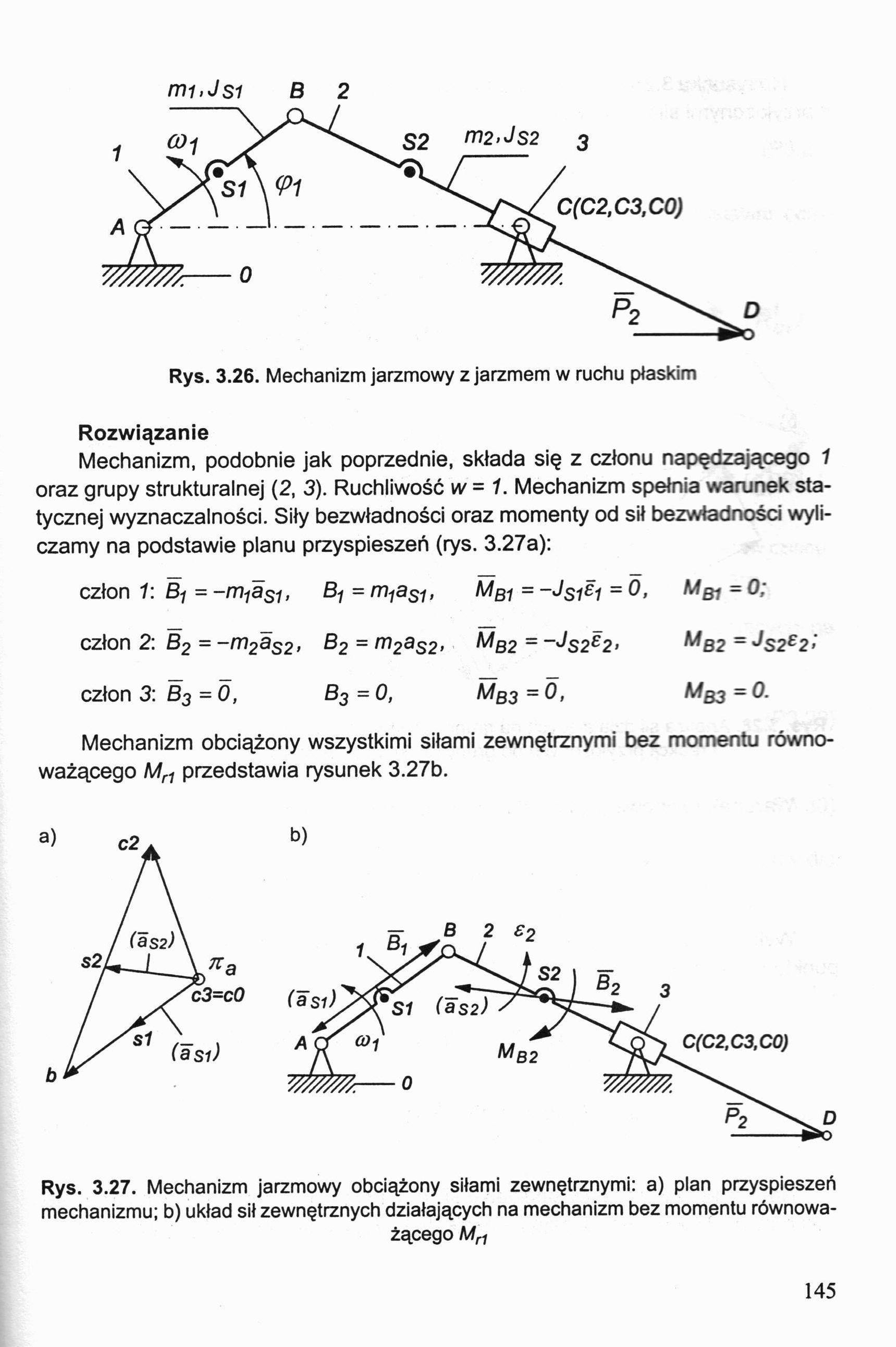
Rozwiązanie

Mechanizm, podobnie jak poprzednie, składa się z członu napędzającego 1 oraz grupy strukturalnej (2, 3). Ruchliwość w = 1. Mechanizm spełnia warunek statycznej wyznaczainości. Siły bezwładności oraz momenty od sił bezwładności wyliczamy na podstawie planu przyspieszeń (rys. 3.27a):

człon 1: B-, =    B-, = m_ta_Sł, M_B1 = -Jsi£i = 0,    = 0;

Człon 2: 63 =-^352'    ^{= m}2^aS2> ^B2⁼~^S2^a2> Mf}2 ⁼ Js2^e2’

człon 3: 63 = 0,    63 - 0,    M33 = 0,    A/f33 = 0.

Mechanizm obciążony wszystkimi siłami zewnętrznymi bez momentu równoważącego M_r1 przedstawia rysunek 3.27b.

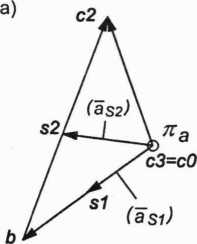
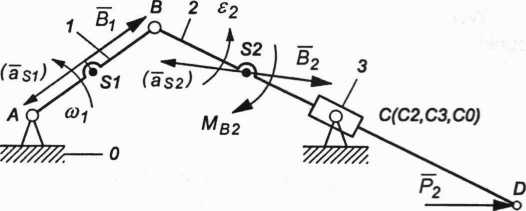
Rys. 3.27. Mechanizm jarzmowy obciążony siłami zewnętrznymi: a) plan przyspieszeń mechanizmu; b) układ sił zewnętrznych działających na mechanizm bez momentu równoważącego M_r1

145