23 luty 07 (67)

Przedstawione na rysunkach 2.15-2.20 plany prędkości i przyspieszeń pozwalają na dokonanie następujących spostrzeżeń:

-    kierunki wszystkich liniowych prędkości bezwzględnych i przyspieszeń bezwzględnych na planie wychodzą z punktów biegunowych ^ n_a;

-    wszystkie liniowe prędkości względne i przyspieszenia względne mają podwójny indeks i łączą końce odpowiednich prędkości lub przyspieszeń bezwzględnych;

-    plan prędkości względnych dowolnej konfiguracji punktów członu sztywnego wykonującego ruch płaski jest podobny do tej konfiguracji punktów i odwrócony względem niej o kąt 90° zgodnie ze zwrotem prędkości członu; przykładem jest podobieństwo figury bek do figury BCK na rysunku 2.17;

-    plan przyspieszeń względnych dowolnej konfiguracji punktów członu sztywnego wykonującego ruch płaski jest podobny do tej konfiguracji punktów i obrócony względem niej o kąt 18CP - 9 zgodnie ze zwrotem przyspieszenia kątowego członu; przykładem jest podobieństwo figury bek do figury BCK na rysunku 2.18;

-    kąt 9 jest to kąt, jaki tworzy wektor przyspieszenia względnego (wektor a_CB) z prostą łączącą dwa wybrane punkty członu (prosta SC), określony równaniem

_tge=^Ł = l2.

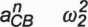
(P2.23)

- dodajemy zawsze do siebie w pierwszej kolejności te prędkości i te przyspieszenia, które są całkowicie znane co do kierunku i wartości, a kończymy rysowanie planu, znajdując punkt przecięcia kierunków prędkości lub przyspieszeń, dla których znany jest tylko ich kierunek, a nie znana ich długość (wartość wektora).

Przykład 2.4

Mechanizm jarzmowy z jarzmem w ruchu płaskim

Wyznaczymy metodą planów prędkości i przyspieszenia liniowe punktów C₂ i D oraz prędkość kątową co₂ i przyspieszenie kątowe e₂ jarzma 2 dla mechanizmu jarzmowego przedstawionego na rysunku 2.21.

Dane: co₁ = const, AB, BD, AC.

Rozwiązanie

Równania planu prędkości

Znajdujemy prędkość punktu 6 należącego do członu napędzającego: Przyjmujemy podziałkę k_v i obliczamy długość rysunkową wektora v_B, tj. (vg):

v_B =co₁ ■ AB

(P2.24)

65