23 luty 07 (87)

Rozwiązanie

Na podstawie rysunku 2.30 zapiszemy równanie wektora promienia wodzącego punktu K

r_K = ^!1 + U    (P2.68)

Następnie wyznaczymy współrzędne wektora r_K:

(P2.69)

r_Kx = I-] coscpt +l₄ cos(ę2 ^+a) r_Ky = I-i sin (pi +I4 sin(ę₂ ^+a)

Zależności (P2.69) są parametrycznymi równaniami toru punktu K, czyli równaniami hodografu wektora promienia wodzącego r_K.

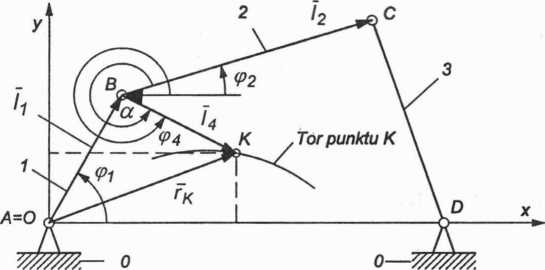
Rys. 2.30. Czworobok przegubowy z oznaczonym punktem K płaszczyzny łącznikowej

Następnie różniczkujemy równania (P2.69) i znajdujemy współrzędne wektora prędkości punktu K:

^vKx

dri

Kx

dt

= -li(Oi sincpi -14(02 sin((p₂ +a)

V_Ky =

dr_Ky

dt

(P2.70)

=! 1(1)1 cosq>i +l₄(o₂ cos((p₂ +a)

Zależności (P2.70) są parametrycznymi równaniami hodografu prędkości v_K. Wartość wektora prędkości punktu K określimy z zależności

v_K=y_{Kx +} v²Ky    (P2.71)

85