23 luty 07 (72)

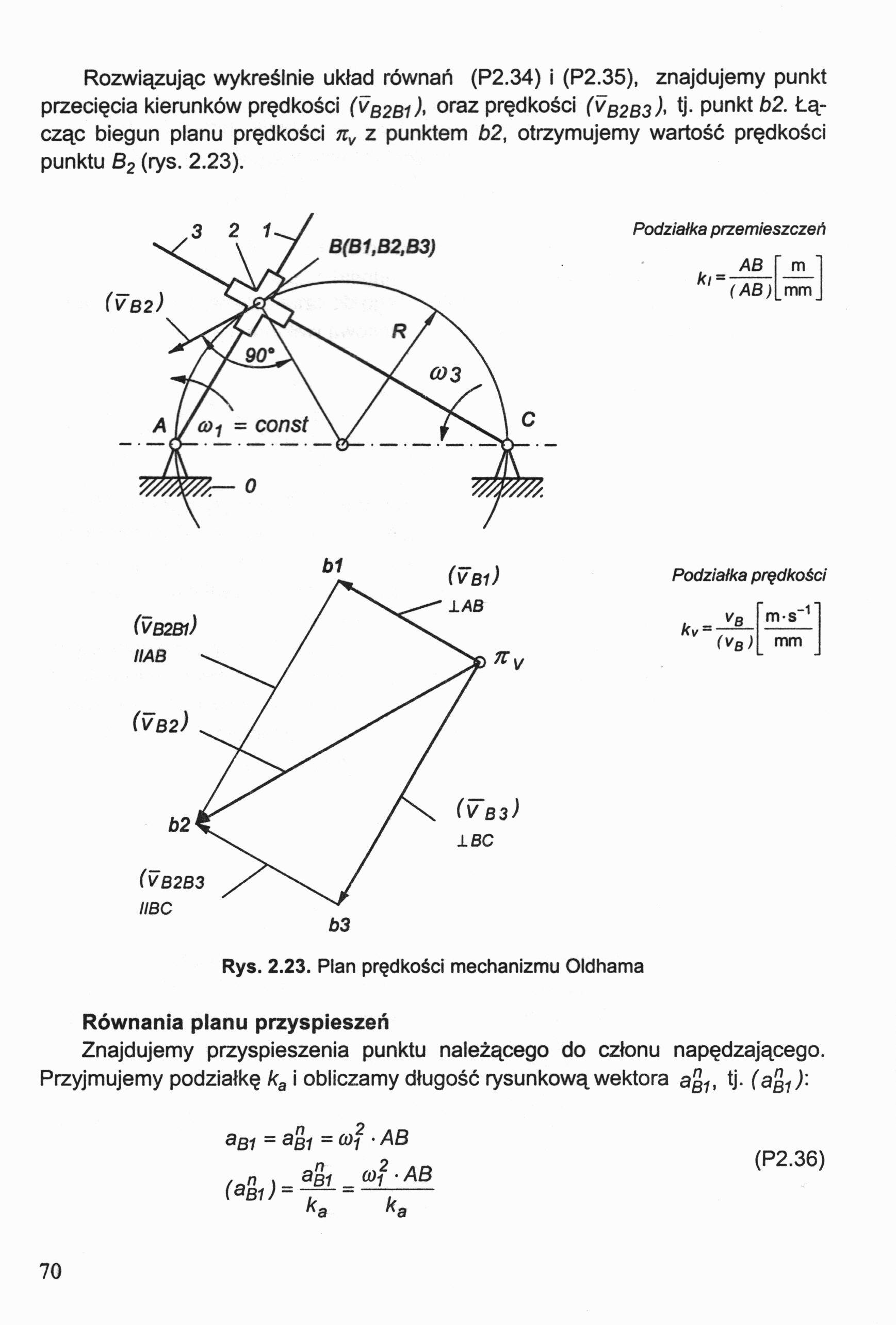
Rozwiązując wykreślnie układ równań (P2.34) i (P2.35), znajdujemy punkt przecięcia kierunków prędkości (v_B2B1 ), oraz prędkości (v_B2B3 )< tj. punkt b2. Łącząc biegun planu prędkości n_v z punktem b2, otrzymujemy wartość prędkości punktu B₂ (rys. 2.23).

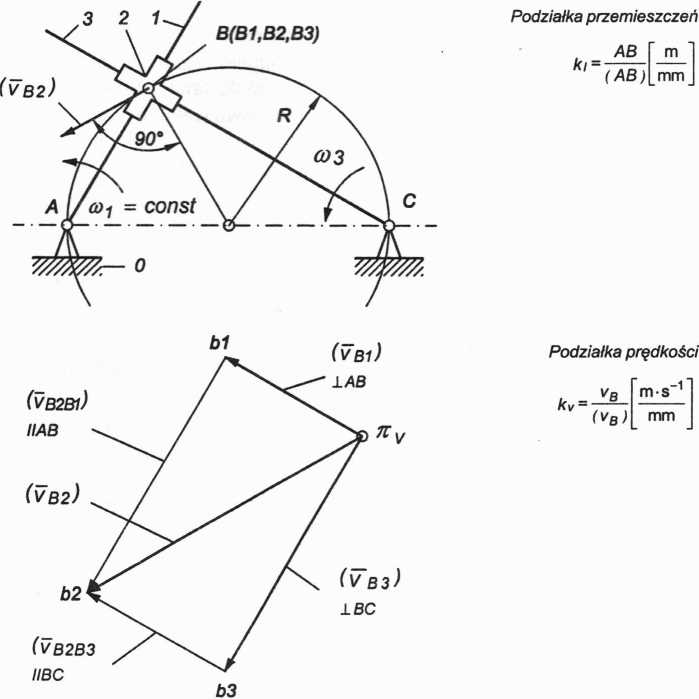
Rys. 2.23. Plan prędkości mechanizmu Oldhama

Równania planu przyspieszeń

Znajdujemy przyspieszenia punktu należącego do członu napędzającego. Przyjmujemy podziałkę k_a i obliczamy długość rysunkową wektora a_B1, tj. (a_B1)'-

^aB1 ⁼ aB1 ~ ^wi '

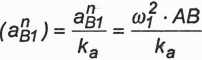
(P2.36)

70