23 luty 07 (84)

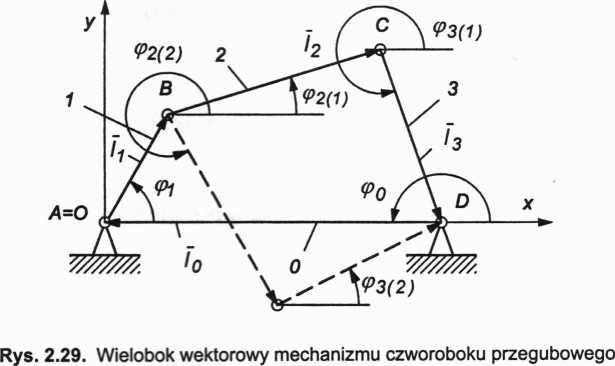
Przekształcamy układ równań (P2.52) do postaci:

If coscpi +l₂ cos(p₂ -1₀ = -l₃ cosę₃

(P2.53)

l₁ sinę-f + l₂sinę₂ = -l₃ sin ę₃

Po wprowadzeniu oznaczeń: A = l-j coscpi-l₀, B = If sin<p₇, otrzymamy:

(P2.54)

A + l₂ cosę₂ = -l₃ cosę₃ B + l₂ sin <P2 -^_l 3 ^s'ⁿ <P3

Równania (P2.54) podnosimy do kwadratu i dodajemy stronami

A² + 2AI₂ cos(p₂ +B² + 2BI₂ sincp₂ +l₂ - /f =0    (P2.55)

Równanie (P2.55) dzielimy przez 2AI₂

A² + B² +1² -1₃    B .

--—*- + cos(p₂ + —sm(p₂ = 0

2 Al 2    A

.    . A² + B² +1² -1₃    _ B

Przyjmiemy oznaczenia: C =____ ——, D = —,

mie postać

2Ah

A

C + cos(p₂ + Dsinę₂ = 0

(P2.56) zatem (P2.56) przyj-(P2.57)

82