23 luty 07 (78)

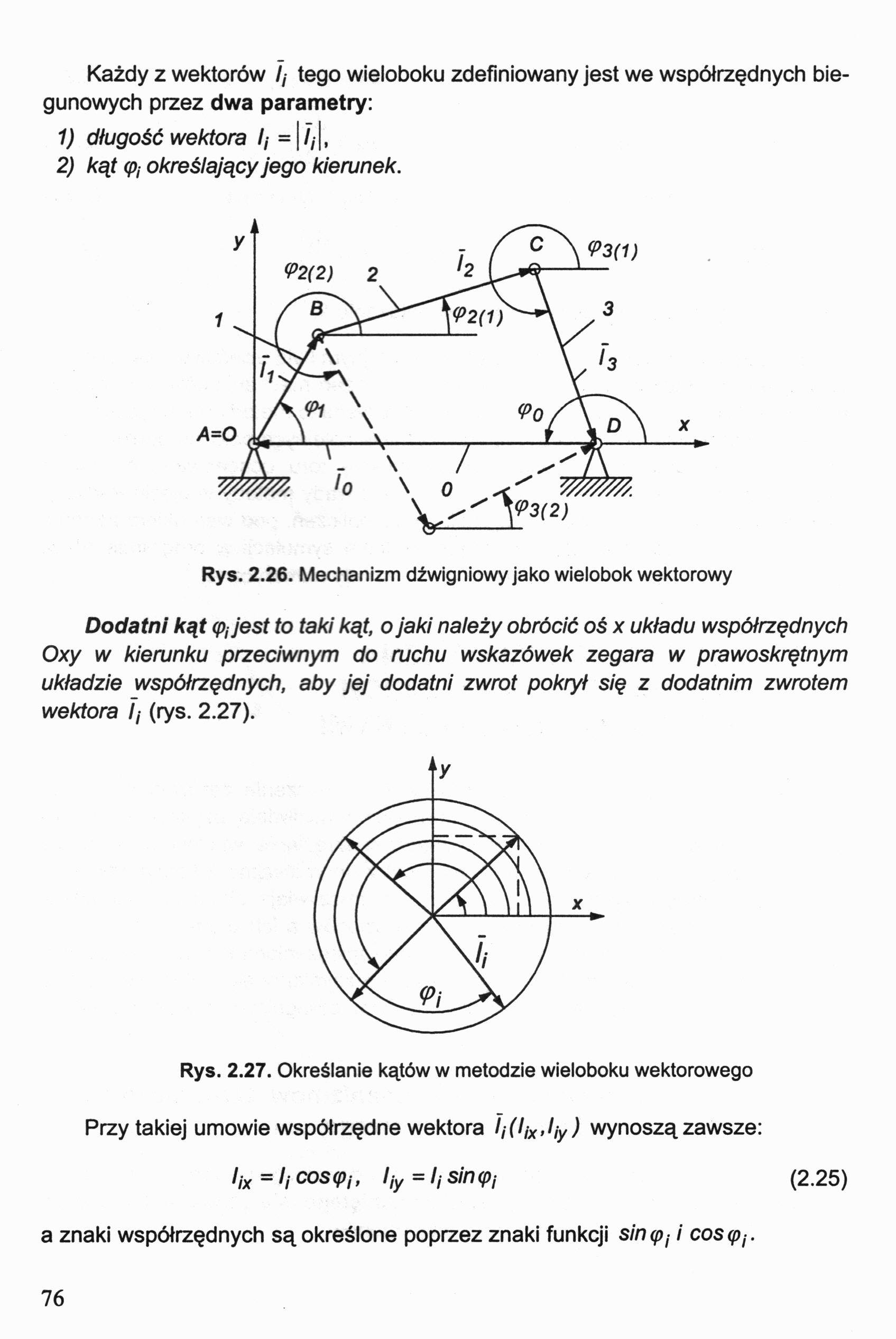
Każdy z wektorów /,- tego wieloboku zdefiniowany jest we współrzędnych biegunowych przez dwa parametry:

1)    długość wektora /,■ =|//|,

2)    kąt q>j określający jego kierunek.

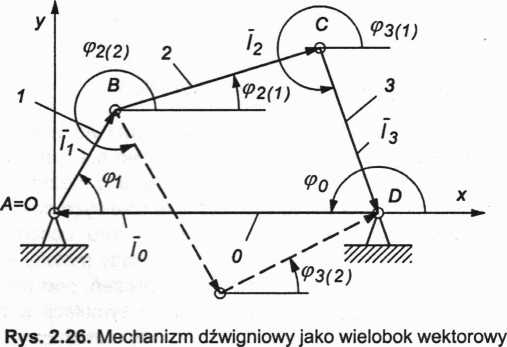
Dodatni kąt (pjjest to taki kąt, o jaki należy obrócić oś x układu współrzędnych Oxy w kierunku przeciwnym do ruchu wskazówek zegara w prawoskrętnym układzie współrzędnych, aby jej dodatni zwrot pokrył się z dodatnim zwrotem wektora Ij (rys. 2.27).

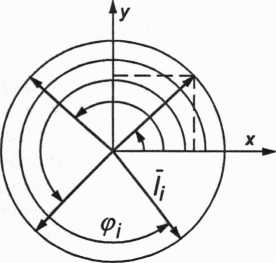
Rys. 2.27. Określanie kątów w metodzie wieloboku wektorowego

Przy takiej umowie współrzędne wektora h(hx>liy) wynoszą zawsze:

l_ix = Ij cos<Pj, l_iy = Ij simpi    (2.25)

a znaki współrzędnych są określone poprzez znaki funkcji s/n<p₍- i cosrp,.

76