23 luty 07 (69)

Rysując wektor (v_DB) z końca wektora (v_B) znajdziemy punkt d stanowiący koniec wektora (v_D). Łącząc biegun planu prędkości n_v z punktem d, otrzymamy prędkość (v_D). Prędkość względną (v_DB) można wyznaczyć również z proporcji

(P2.27)

(v_DB) db _ (PB) (^vC2b) °2b (CB)

Równania planu przyspieszeń

Znajdujemy przyspieszenie punktu należącego do członu napędzającego. Przyjmujemy podziałkę k_g i obliczamy długość rysunkową wektora a_B, tj. (a_B).

a_B = ag = cof ■ AB

<^P228>

^Ka

Ponieważ suwak obraca się razem z jarzmem, to jego przyspieszenie kątowe jest równe przyspieszeniu kątowemu jarzma, czyli e₂ =£3- W celu znalezienia przyspieszeń liniowych należy rozwiązać układ równań (P2.29), porównując ich prawe strony.

(SC2) ~(^aB) ⁺ (&C2B ) + (3,Q2B )

(P2.29)

II AB IIBC 1BC (^aC2 ) ⁼ (^aC3) ⁺ (^aC2C3 ) ⁺ (^aC2C3 ) = 0    18C    II BC

gdzie: (aⁿC2B) =

(o₂ BC

f^cor i _ ^2co2 ■ (^VC2C3 )' ^kv '^aC2C3> ~    Z

Zauważymy, że w tym przypadku v_c2c3 = v_C2 zgodnie z równaniem (P2.25). Rozwiązaniem układu równań (P2.29) jest plan przyspieszeń przedstawiony na rysunku 2. 22. Korzystając z planu przyspieszeń znajdziemy przyspieszenie kątowe

(P2.30)

(P2.31)

_ (^aC2B ^S2--BC

Następnie wyznaczymy przyspieszenie punktu D z równania (³d)- (^aB ) (^aDB ) ^ (^aDB ) IIBD 1BD

gdzie: (a_BB) =

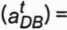
e₂ - BD

^ka

67