23 luty 07 (64)
Przyspieszenie punktu K można również znaleźć, obliczając w pierwszym
6 • BK
zrównać (P2.18) przyspieszenie względne styczne (a(KB) = —-, wówczas
ka
w równaniu pozostaną tylko dwie niewiadome: wartość i kierunek (a K).
Przykład 2.3
Mechanizm jarzmowy z suwakiem w ruchu płaskim
Wyznaczymy metodą planów prędkość i przyspieszenie liniowe punktu B oraz prędkość kątową co3 i przyspieszenie kątowe e3 jarzma 3 dla mechanizmu jarzmowego przedstawionego na rysunku 2.19,
Dane: co, = const, AC, BC.
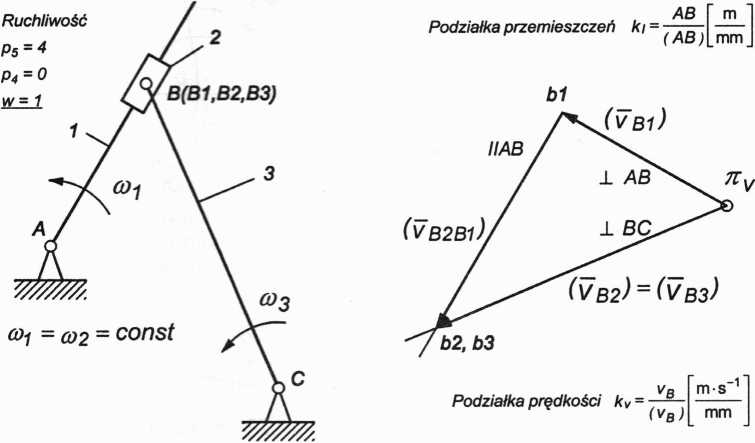
Rys. 2.19. Plan prędkości mechanizmu jarzmowego
Rozwiązanie
Równania planu prędkości
Znajdujemy prędkość punktu B-, należącego do członu napędzającego. Przyjmujemy podziałkę kv i obliczamy długość rysunkową wektora vB1, tj. (vB1):
VB1 -^1 'AB
(P2.19)
(**<>=vt
KV
Ponieważ suwak porusza się po prostoliniowej prowadnicy, to jego prędkość kątowa jest równa prędkości kątowej prowadnicy co., = w2.
62
Wyszukiwarka
Podobne podstrony:
23 luty 07 (70) Przyspieszenie względne (aDB) można wyznaczyć również na podstawie znajomości długoś
23 luty 07 (45) Przyspieszenie dowolnego punktu K wyraża się wzorem (2.4) aK=aU+aW = a01 + aK01 +
23 luty 07 (43) Przyspieszenie kątowe: (2.2c) (2.2d) (2.2e) (2-2f) e(t) = (0,0,e(t)), e(t) = ^ = ^-
23 luty 07 (52) Przyspieszenie Coriolisa acor =0, gdy: cou =0, lub vw =0 lub vwHwu. Ostatni przypade
23 luty 07 (61) Prędkość punktu K znajdziemy na podstawie układu równań (P2.13), porównując ich praw
23 luty 07 (105) Ostatecznie przełożenie przekładni obiegowej wyniesiez3y Zj+z3 Zł) Z1 (P2.97) Przeł
23 luty 07 (130) Jeżeli w mechanizmie zastąpimy pary kinematyczne ki. 4 parami ki. 5, to równanie (3
23 luty 07 (39) Stosowane są również metody grafoanalityczne, które w zasadzie można zaliczyć do met
23 luty 07 (66) Łącząc biegun planu przyspieszeń na z punktem przecięcia b2 otrzymamy wartość przysp
23 luty 07 (73) Następnie zapisujemy równanie przyspieszenia punktu B2, który znajduje się na członi
23 luty 07 (108) Rozwiązanie Przełożenie przekładni można zapisać /)3 = —. 3j Wykorzystamy wzór na
23 luty 07 (117) Siły wewnętrzne, czyli reakcje w parach kinematycznych, oznaczono symbolami, które
23 luty 07 (42) W ruchu postępowym przewodnia prędkości i przewodnia przyspieszeń prostej ruchomej,
23 luty 07 (44) W ruchu obrotowym przewodnia prędkości i przewodnia przyspieszeń prostej ruchomej są
23 luty 07 (47) Przewodnia przyspieszeń obrotowego ruchu względnego Składanie przyspieszenia unoszen
23 luty 07 (48) Prędkość vB i przyspieszenie aB wynikają z postępowego ruchu unoszenia, prędkość vCB
23 luty 07 (53) Rys. 2.13. Składowe przyspieszeń suwaka 2 poruszającego się po prostoliniowej prowad
23 luty 07 (54) graficzne wektorów prędkości i przyspieszeń stanowiących odpowiedniki wektorów rzecz
23 luty 07 (55) Oznacza to, że długości rysunkowe wektorów prędkości liniowej oraz przyspieszenia li
więcej podobnych podstron