23 luty 07 (66)
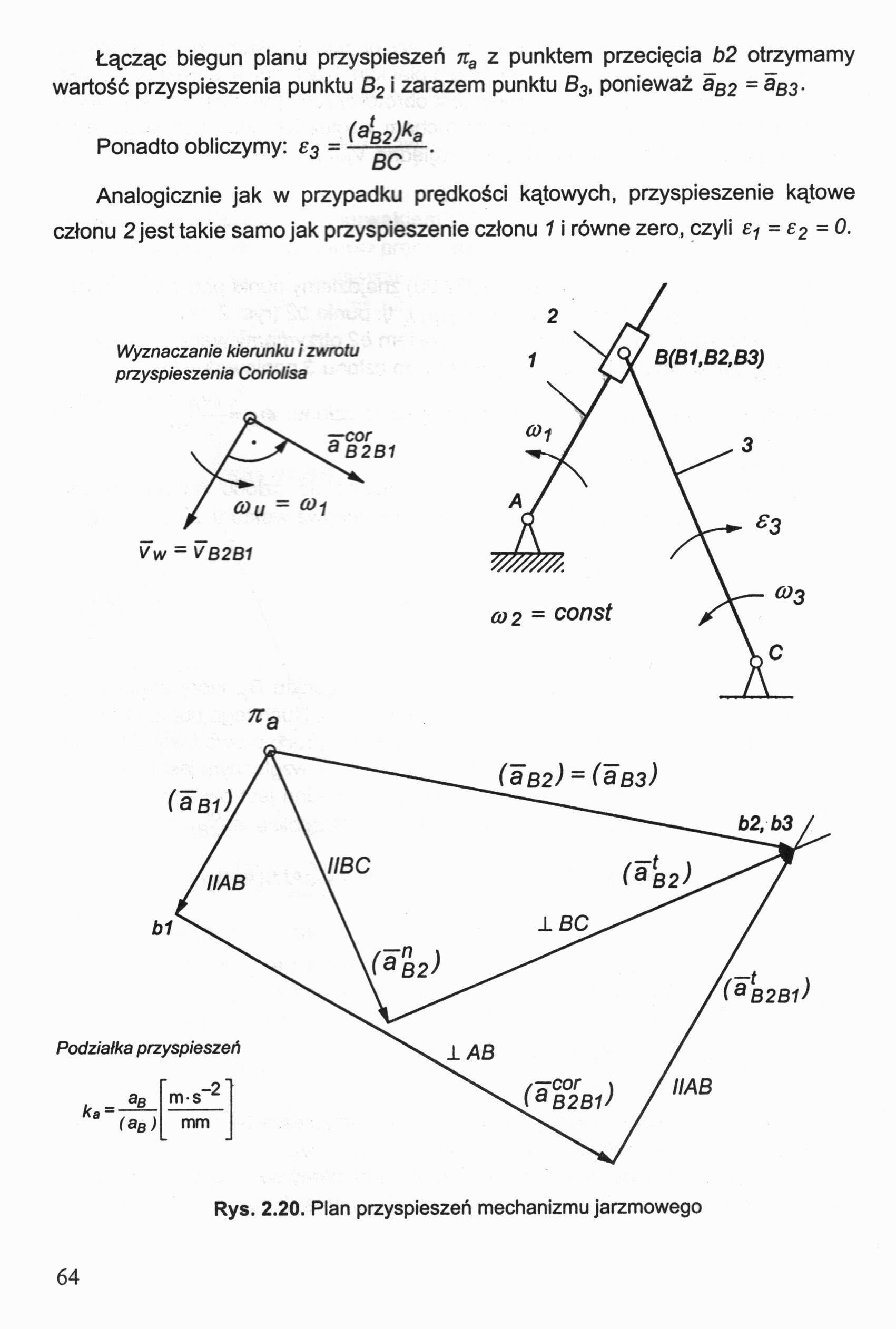
Łącząc biegun planu przyspieszeń na z punktem przecięcia b2 otrzymamy wartość przyspieszenia punktu B2 i zarazem punktu S3, ponieważ aB2 = aB3.
(atB2)^a BC '
Ponadto obliczymy: e3 =
Analogicznie jak w przypadku prędkości kątowych, przyspieszenie kątowe członu 2 jest takie samo jak przyspieszenie członu 1 i równe zero, czyli e? = e2 = 0.
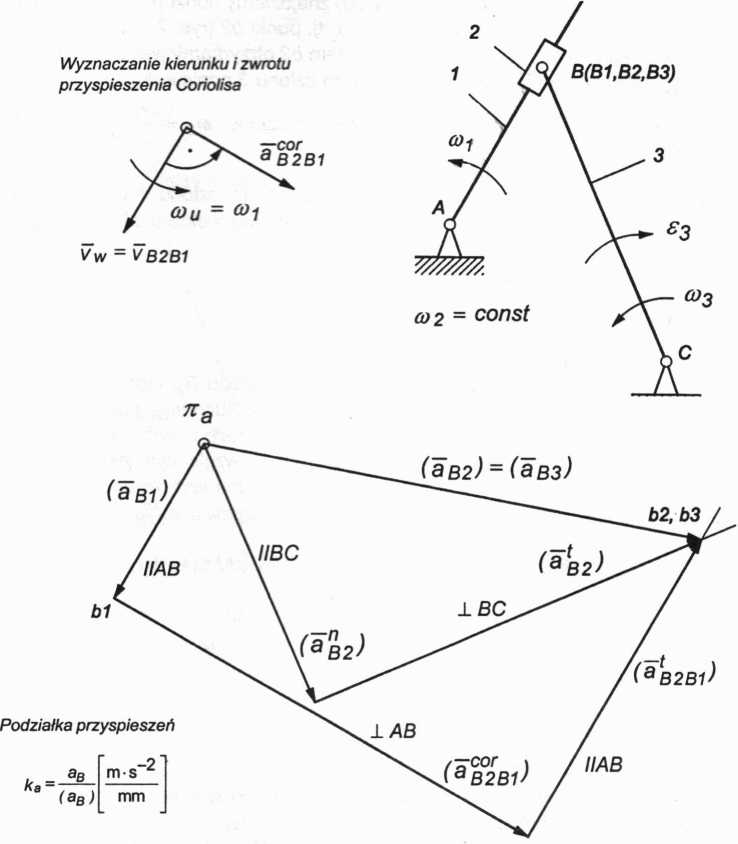
Rys. 2.20. Plan przyspieszeń mechanizmu jarzmowego
64
Wyszukiwarka
Podobne podstrony:
23 luty 07 (73) Następnie zapisujemy równanie przyspieszenia punktu B2, który znajduje się na członi
23 luty 07 (53) Rys. 2.13. Składowe przyspieszeń suwaka 2 poruszającego się po prostoliniowej prowad
23 luty 07 (54) graficzne wektorów prędkości i przyspieszeń stanowiących odpowiedniki wektorów rzecz
23 luty 07 (59) Rys. 2.16. Plan przyspieszeń punktów mechanizmu korbowo-suwakowego Rozwiązujemy wykr
23 luty 07 (116) a) b) P 3 Rys. 3.1. Siły zewnętrzne działające na mechanizm korbowo-suwakowy Objaśn
23 luty 07 (148) Równanie równowagi sił działających na człon napędzający ma postać R21 + Bi + Rqi +
23 luty 07 (58) W wyniku przecięcia kierunków (vc) i (vCB) otrzymamy punkt c. Odcinek łączący biegun
23 luty 07 (63) Na przecięciu kierunków przyspieszeń (afKB) i (afKC) otrzymamy punkt k. Biegun na łą
23 luty 07 (69) Rysując wektor (vDB) z końca wektora (vB) znajdziemy punkt d stanowiący koniec wekto
23 luty 07 (133) Rozwiązanie w układzie płaskim dowolnego równania wektorowego, czyli narysowanie pl
23 luty 07 (42) W ruchu postępowym przewodnia prędkości i przewodnia przyspieszeń prostej ruchomej,
23 luty 07 (43) Przyspieszenie kątowe: (2.2c) (2.2d) (2.2e) (2-2f) e(t) = (0,0,e(t)), e(t) = ^ = ^-
23 luty 07 (44) W ruchu obrotowym przewodnia prędkości i przewodnia przyspieszeń prostej ruchomej są
23 luty 07 (45) Przyspieszenie dowolnego punktu K wyraża się wzorem (2.4) aK=aU+aW = a01 + aK01 +
23 luty 07 (47) Przewodnia przyspieszeń obrotowego ruchu względnego Składanie przyspieszenia unoszen
23 luty 07 (48) Prędkość vB i przyspieszenie aB wynikają z postępowego ruchu unoszenia, prędkość vCB
23 luty 07 (52) Przyspieszenie Coriolisa acor =0, gdy: cou =0, lub vw =0 lub vwHwu. Ostatni przypade
23 luty 07 (55) Oznacza to, że długości rysunkowe wektorów prędkości liniowej oraz przyspieszenia li
23 luty 07 (56) Kolejność postępowania w metodzie planów prędkości i przyspieszeń: 1. &n
więcej podobnych podstron