23 luty 07 (56)

Kolejność postępowania w metodzie planów prędkości i przyspieszeń:

1.    należy narysować mechanizm w podziałce k, w położeniu przewdzianym do analizy kinematycznej;

2.    określić ruchliwość i klasę mechanizmu;

3.    wskazać człon lub człony napędzające;

4.    oznaczyć cyframi człony mechanizmu, poczynając od członu napędzającego;

5.    oznaczyć dużymi literami istotne punkty mechanizmu;

6.    określić parametry kinematyczne członu napędzającego;

7.    napisać równania wektorowe określające relacje pomiędzy prędkościami punktów mechanizmu;

8.    rozwiązać wykreślnie równania wektorowe, rysując w podziałce k_v odpowiednie wieloboki wektorowe na tzw. planie prędkości, wychodząc z jednego punktu biegunowego;

9.    analogiczne rozwiązać zadanie dotyczące przyspieszeń korzystając z wartości wyznaczonych na podstawie planu prędkości i narysować je w postaci tzw. planu przyspieszeń w podziałce k_a.

Metoda planów prędkości i przyspieszeń zostanie przedstawiona na przykładach dla wybranych mechanizmów.

Przykład 2.1

Mechanizm korbowo-suwakowy

Wyznaczymy metodą planów prędkości i przyspieszenia liniowe punktów 6, C oraz K oraz prędkość kątową co₂ i przyspieszenie kątowe łącznika e₂ dla mechanizmu korbowo-suwakowego przedstawionego na rysunku 2.15.

Dane: w-f = const, AB, BC, BK.

Rozwiązanie

Mechanizm rysujemy w podziałce k_h Obliczamy ruchliwość mechanizmu:

n = 3, p_s = 4, p₄ = 0, stąd w = 3n-2p₅-p₄ = 1.

Członem napędzającym jest człon 1.

Równania planu prędkości

Obliczamy prędkość punktu 6 należącego do członu napędzającego 1 i zarazem do łącznika 2 mechanizmu korbowo-suwakowego. Przyjmujemy podziałkę k_v obliczamy długość rysunkową wektora v_B, tj. (v_B):

v_B=co₁ ■ AB

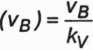
(P2.1)

54