23 luty 07 (21)

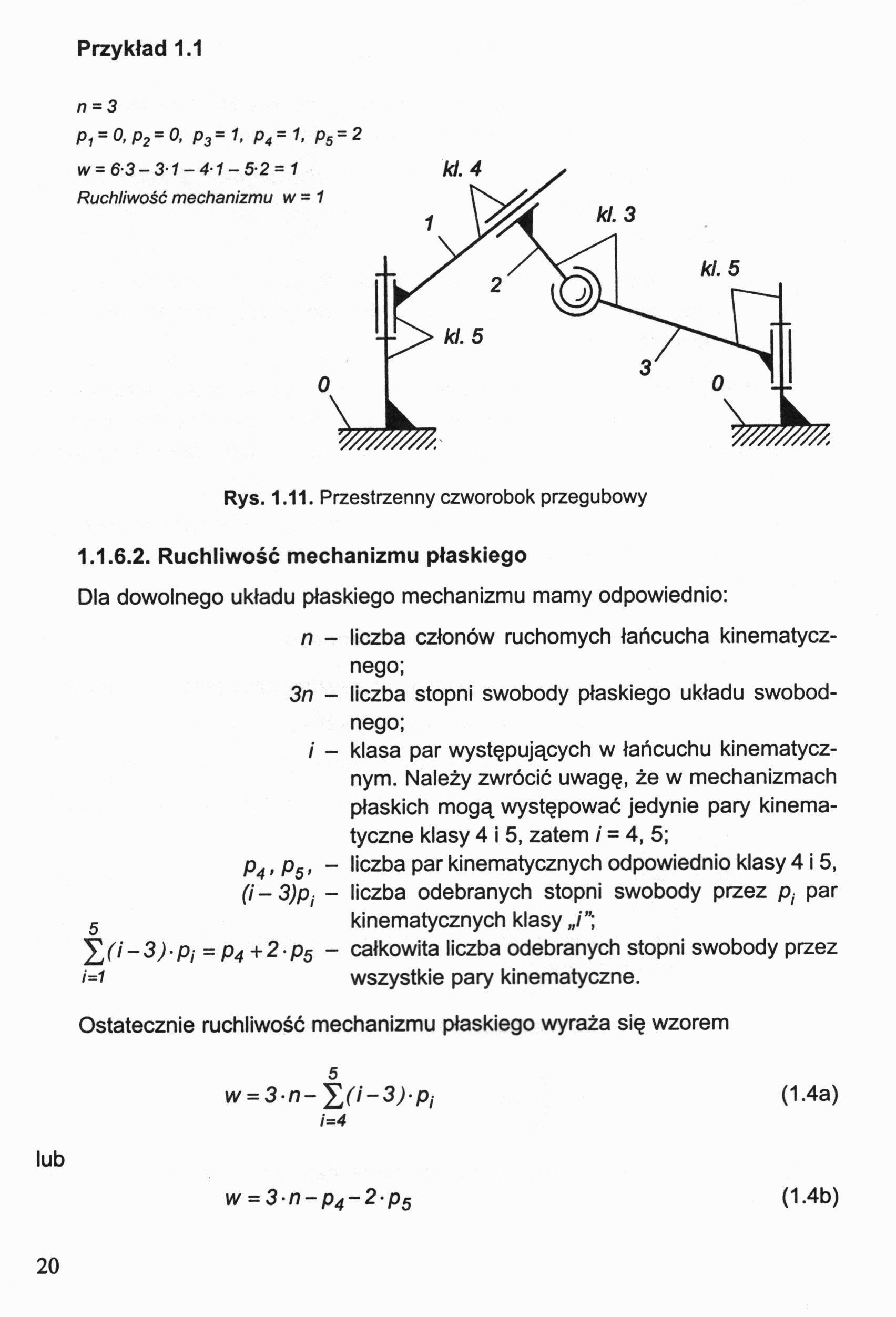
Przykład 1.1 n = 3

p₁ = 0,p₂ = 0, p₃= 1, p₄=1, p_s=2

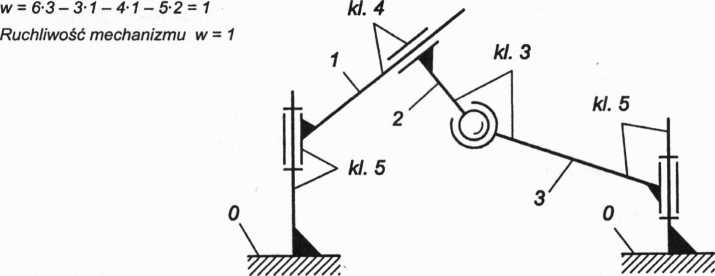
Rys. 1.11. Przestrzenny czworobok przegubowy

1.1.6.2. Ruchliwość mechanizmu płaskiego

Dla dowolnego układu płaskiego mechanizmu mamy odpowiednio:

n

3n

i

P4' P5'

0~3)p,

5

J_J(i-3)-p_i=p₄+2p₅

i=1

liczba członów ruchomych łańcucha kinematycznego;

liczba stopni swobody płaskiego układu swobodnego;

klasa par występujących w łańcuchu kinematycznym. Należy zwrócić uwagę, że w mechanizmach płaskich mogą występować jedynie pary kinematyczne klasy 4 i 5, zatem / = 4, 5; liczba par kinematycznych odpowiednio klasy 4 i 5, liczba odebranych stopni swobody przez p, par kinematycznych klasy „/”;

całkowita liczba odebranych stopni swobody przez wszystkie pary kinematyczne.

Ostatecznie ruchliwość mechanizmu płaskiego wyraża się wzorem

w = 3-n-J_J(i-3)-p_j

i=4 lub

w = 3-n-p₄-2p₅

(1 -4a)

(1.4b)

20