23 luty 07 (140)

Przykład 3.3

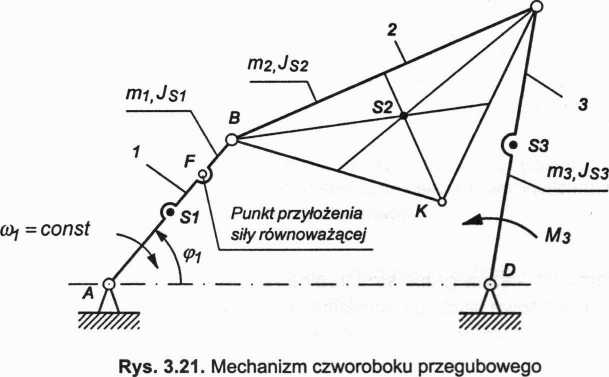
Mechanizm czworoboku przegubowego

Przeprowadzić analizę kinetostatyczną mechanizmu czworoboku przegubowego metodą grafoanalityczną w położeniu zadanym na rysunku 3.21. Wyznaczyć reakcje dynamiczne w parach kinematycznych oraz siłę równoważącą P_r1 przyłożoną do korby 1 w punkcie F. Tarcie w parach kinematycznych należy pominąć. Dane: prawo ruchu członu napędzającego, o)₁ = const, ę_1t długości członów AB, AR    CD

BC, CD, BK, CK, AS-, = —, DS₃=—. Środek masy łącznika S₂ znajduje się

w punkcie przecięcia środkowych trójkąta BCK. Masy członów są równe: m_1t m₂, m₃, a momenty bezwładności członów względem środków mas: J_S1, J_S2, J_S3. Moment oporu użytecznego wynosi M₃. Mechanizm porusza się w płaszczyźnie poziomej.

C

Rozwiązanie

Mechanizm składa się z członu napędzającego 1 i z grupy strukturalnej (2, 3) kl. 2. Ruchliwość mechanizmu jest równa w = 1. Mechanizm spełnia warunek statycznej wyznaczalności. Przyspieszenia środków mas a_s1, a_S2, a_S3 oraz przyspieszenia kątowe członów zostały wyznaczone na podstawie planu przyspieszeń (rys. 3.22a).

Obliczamy siły bezwładności oraz momenty od sił bezwładności: człon 1: B-j = -mia$i, Bf = m-ja₃f, Mgf = -Jsi&i ⁼ 0,    = 0;

człon 2: B₂ =-m₂a₃₂, B₂ = m₂a₃₂,    Mq₂ = ~Js2^2<    ^B2 ⁼^S2^e2<

człon 3: B₃ = -m₃as₃, B₃ = m₃a_S3,    M_B3 = -Js3^3<    ^mB3 = ^JS3^e3-

139