24 luty 07 (40)

Rozwiązanie

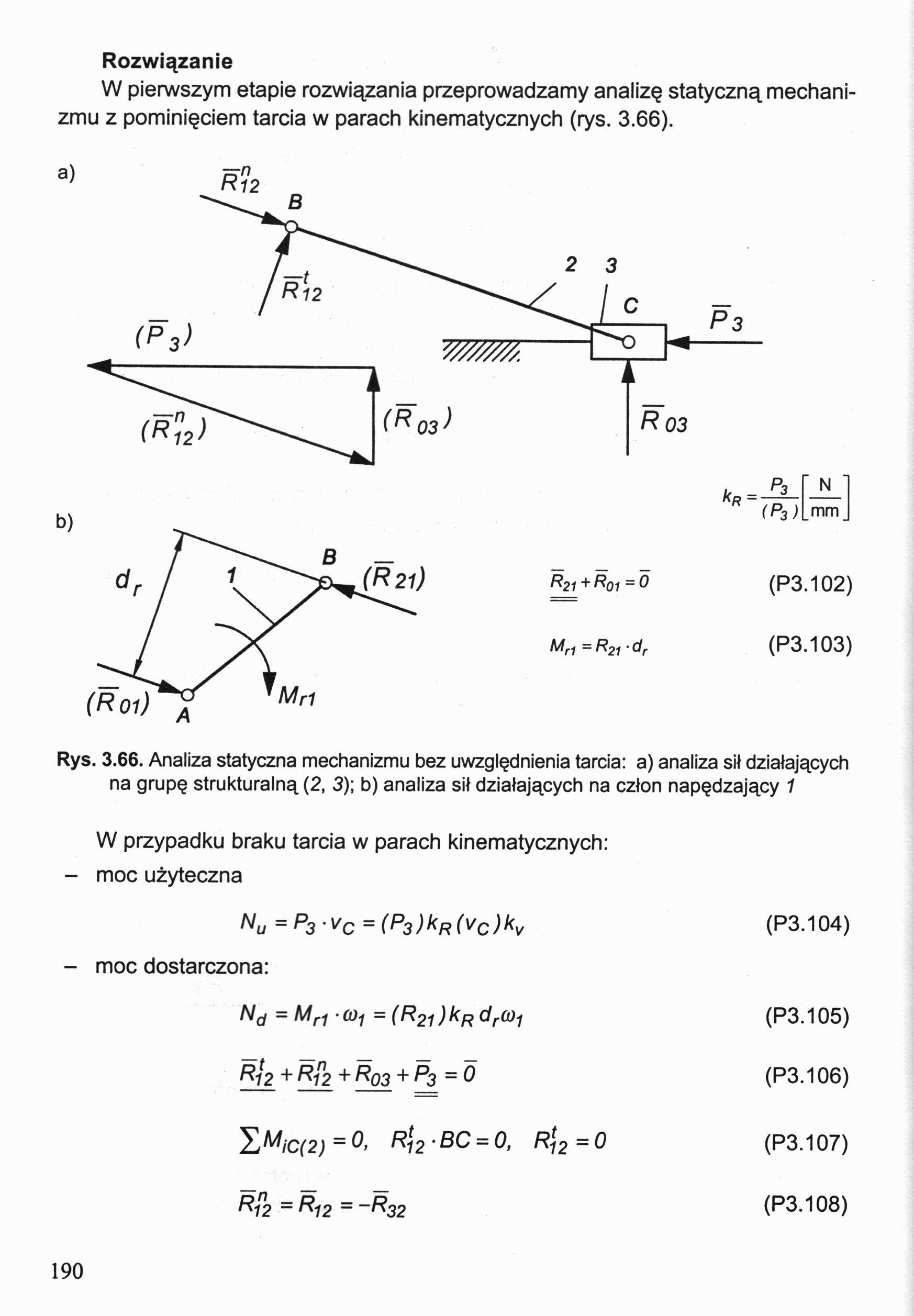
W pierwszym etapie rozwiązania przeprowadzamy analizę statyczną mechanizmu z pominięciem tarcia w parach kinematycznych (rys. 3.66).

R12

Rys. 3.66. Analiza statyczna mechanizmu bez uwzględnienia tarcia: a) analiza sił działających na grupę strukturalną (2, 3); b) analiza sił działających na człon napędzający 1

W przypadku braku tarcia w parach kinematycznych:

-    moc użyteczna

N_u=P₃-v_c=(P₃)k_R(v_c)k_v    (P3.104)

-    moc dostarczona:

Nrf = M_rf ■ Wi = (R21 )k_R d_r(i>i    (P3.105)

Rj2+R^ + Ro3 + P₃ =Ó    (P3.106)

lMi_C(2) = 0, R\₂BC = 0, R*2 = 0    (P3.107)

Rfe = R₁₂ = -R₃₂    (P3.108)

190