mechanika77

przy czym: — rys. 2.23a	«l = «A^+*<>	«2 * «A “ ^	<^a* ^> <0	<2.5*1)
- rys. 2.23b	^= «A^+«<>	II 1	O V <	(2.60)
2.1.4. KINEMATYKA CIAŁA SZTYWNEGO W RUCHU KULISTYM

Mtyspić s zen i e k ątowe

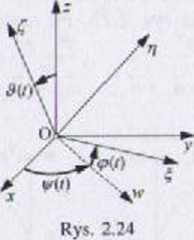
Ruchem kulistym bryły (ciała sztywnego) nazywamy taki ruch. podczas któro go jeden punkt ciała pozostaje nieruchomy. W punkcie tym przyjmujemy I początek O nieruchomego układu współrzędnych xyz. Z bry łą związany jesi ¹ ruchomy układ współrzędnych £tić, o początku O. Współrzędnymi ruchu kulistego są kąty Eulera (rys. 2.24):

©(/) - kąt nutacji (między osiami z. ().

\p(r) - kąt precesji (między osiami x, w),

<p(r) - kąt obrotu własnego (między osiami w, £ ),

gdzie w jest tzw. osią węzłów, pokrywającą się z krawędzią przecięcia płasz czyzn xy oraz . Jeśli <p = 0. to w = £.

Ruch kulisty można zinterpretować jako ruch bryły wokół chwilowej osi obro tu u (o położeniu zmiennym w- czasie), rys. 2.25a. Chwilowa prędkość kątowa jest sumą trzech nieorlogonalnych wektorów, rys. 2.25b:

<3 =    ♦ lj ^ = u)_#e_w + ia_%e. ♦ <a^e_c    (2.61)

gdzie: to_e = 6 — prędkość kątowa nutacji.

= ip — prędkość kątowa precesji. o>_T = (p - prędkość kątowa obrotu własnego.

(2.62)

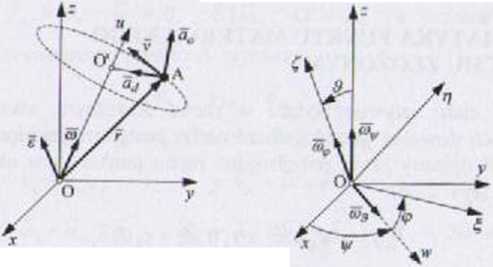
Rys. 2.25

[ Dowolny punkt bryły A porusza się po chwilowej trajektorii kołowej " środku O', leżącej w płaszczyźnie prostopadłej do chwilowej osi obrotu u. Prędkość i przyspieszenie punktu A określają wzory

v = w x r. a = a₉+ a_Jt    a_a = e x r, a_d - w x v (2.63)

prędkość kątowa u> jeży na osi u. Przyspieszenie kątowe e nic jest kolinear-m- / ń>. Prędkość v punktu A jest styczna do chwilowej trajektorii ruchu punktu A. Przyspieszenie obrotowe a_Q nie jest styczne do chwilowej trajekto-;fn ruchu punktu A. Przyspieszenie dośrodkowe a_d jest skierowane do punktu • l'. a więc a_d ± v.

Aksoidą stałą (AS) nazywamy powierzchnię stożkową, utworzoną prze/ Chwilową oś obrotu w czasie, w układzie xyz. Aksoidą ruchomą (AR) nazywamy powierzchnię stożkową, utworzoną przez chwilową oś obrotu w czasie, w układzie W każdej chwili aksoidy AS, AR są do siebie styczne

Precesją regularną nazywamy ruch kulisty spełniający następujące warun-Iti. rys. 2.25:

0 = const	-*	“o	- 0
♦ (0 ^3 <*V ^+	=>		= const	(2.64)
«P<0 " <V + <p0			= const

154

Kinematyka. hniMawy teorii y./iw i (Onematyka. Pochtawy Icomyc/nc

155