mechanika140

Punkt materialny jest obciążony tylko silą ciężkości G • mg, stąd składowe siły czynnej:

P_t = 0, P_y = -G - -mg Wyznaczenie x(t\ y{t):

Q_x -0 —> x(t) « V ^{+ x}o * (V₀COSB₀)f    (I)

t

Q_y{t) - -[mgdr * mgr —♦

o

=■> y(0 * —[(-mgt)dt + }_Qt + y₀ = -~g'²⁺(v₀sina₀)f    (2)

w^J    z

Wyznaczenie prędkości v(f):

i(0 = v₀cosa_Q, y(f) = -gr + v₀sina₀

v(t) *    ⁺ 5W ⁼ \^o cos²a₀ *[v₀sma₀ - gif

Wyznaczenie toru ruchu: 0) => x = rv₀cosa₀

(2) -» y

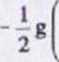
^vo^cosoct

:(v₀coscc₀)

₊ v₀sina₀

X

v₀cosa₀

v₀cosa₀

= xtga₀-x² ₂^g — =/U)

2Vg cos² a₀

Wyznaczenie wysokości h i zasięgu d\ y * f(x) -    * bx * c (parabola drugiego stopnia)

a ---$-b = tga₀, c = 0

2 v² cos² a₀

Wyznaczenie współrzędnych wierzchołka paraboli:

d

2

d

h

2a

■2, tgcc₍

sina.

cos a,

b =	sin a0 2v0^Ł cos^2	«o	= — • 2 sin
a	cosa0 g		g
A	b~ Aac	-b^2	sin^2a0
Aa	Aa	4«	cos^2 ccn

— sin2a,

g

4g

2g

280

Dynamika. 3.2 I Dynamika punkin materiulnegn bat wfc'<V*

Zadanie* 3.13

ocisk o masie m wystrzelono z prędkością początkową v_Q. pod kątem a₀ do poziomu. Wyznaczyć współrzędne ruchu pocisku y{t) oraz równanie t»>ru y =/(jr). Siła oporu powietrza wynosi R[t) = -Pmy(/), gdzie p ;s ¹

związanie

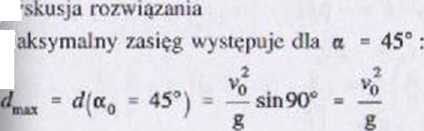
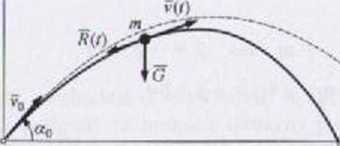
Siła R(t) jest kolincama z wektorem prędkości v(/) i ma przeciwny zwrot, ocisk traktujemy jako punkt materialny poruszający się w płaszczyźnie xy. Siły czynne obciążające masę m oraz przybliżony tor ruchu pocisku pokazano im poniższym schemacie. Linią przerywaną zilustrowano tor ruchu w przypadku braku siły oporu powietrza.

V

d

X

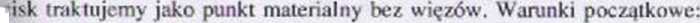
'(, = 0.    >0 * *o ^{= v}o^cosao» y₀ - ^v0^sina0

Siła czynna:

ł\t) ■ C + /?(f) =>

P_t(t) = -pmi(f)

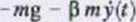
w noniu ruchu i ich dwukrotne całkowanie oznaczone [1]:

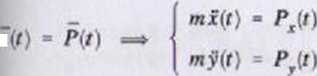
(1)

(2)

281

lurmk.i 12.1. I>ytiiimik:i punktu materialnego btv widzów