Mechanika ogolna0007

14

14

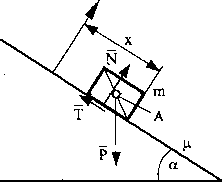
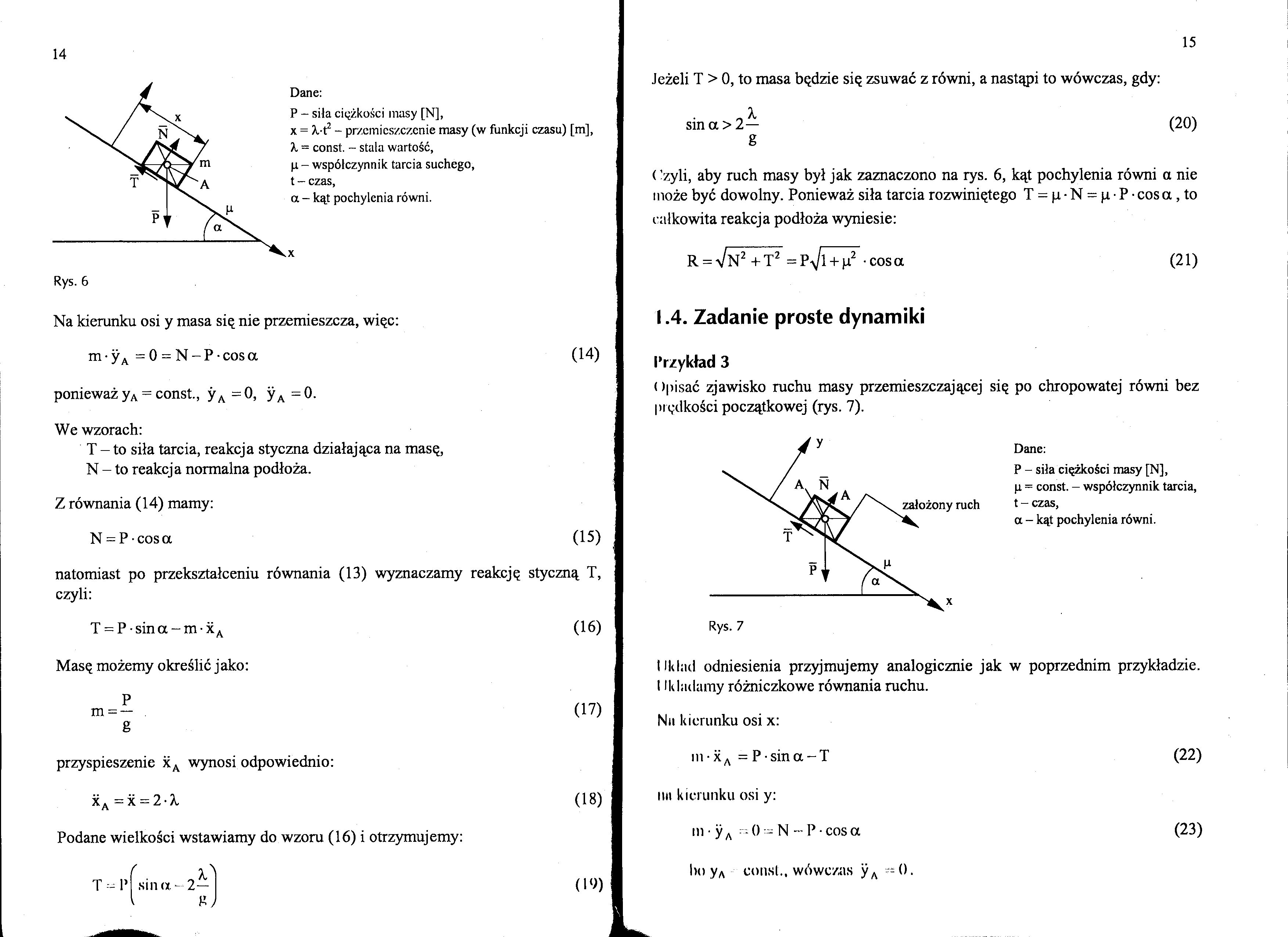
Rys. 6

Dane:

P - siła ciężkości masy [N],

x = X-t² - przemieszczenie masy (w funkcji czasu) [m], X = const. - stała wartość, p - współczynnik tarcia suchego, t - czas,

a - kąt pochylenia równi.

\x

(14)

Na kierunku osi y masa się nie przemieszcza, więc: m • y_A = 0 = N - P • cos a

ponieważy_A = const., y_A =0, y_A =0.

We wzorach:

T - to siła tarcia, reakcja styczna działająca na masę,

N - to reakcja normalna podłoża.

Z równania (14) mamy:

N = P-cosa    (15)

natomiast po przekształceniu równania (13) wyznaczamy reakcję styczną T, czyli:

T = P-sina-m-x_A    (16)

Masę możemy określić jako:

m =

P

g

(17)

przyspieszenie x_A wynosi odpowiednio:

(18)

x_A = x = 2 • A,

Podane wielkości wstawiamy do wzoru (16) i otrzymujemy:

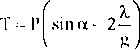
(ló)

Jeżeli T > O, to masa będzie się zsuwać z równi, a nastąpi to wówczas, gdy:

sin a >2—    (20)

g

('żyli, aby ruch masy był jak zaznaczono na rys. 6, kąt pochylenia równi a nie może być dowolny. Ponieważ siła tarcia rozwiniętego T = p ■ N = p ■ P ■ cos a , to całkowita reakcja podłoża wyniesie:

R = Vn² +T² =P^l + p² cosa    (21)

1.4. Zadanie proste dynamiki

Przykład 3

(łpisać zjawisko ruchu masy przemieszczającej się po chropowatej równi bez prędkości początkowej (rys. 7).

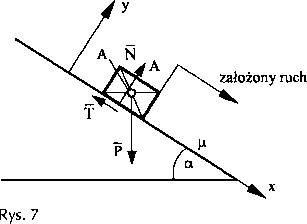
Dane:

P - siła ciężkości masy [N], p. = const. - współczynnik tarcia, t - czas,

a - kąt pochylenia równi.

Układ odniesienia przyjmujemy analogicznie jak w poprzednim przykładzie. I Ikladamy różniczkowe równania ruchu.

Na kierunku osi x:

m-x_A = Psina-T    (22)

im kierunku osi y:

m ■ y_A • 0 - N - P-cosa

Iło y_A const., wówczas y_A =0.

(23)