Mechanika ogolna0031

62

Na krążek działa siła ciężkości Q przyłożona w środku masy krążka, czyli w punkcie A. Różniczkowe równanie ruchu krążka będzie miało postać:

I_A -jp = M-T-r.

Siła tarcia wyraża się następująco:

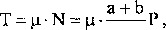
a

ponieważ z równowagi dźwigni dostaniemy: N =

a + b

P.

a

Moment bezwładności określimy następująco:

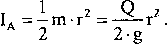
Równanie ruchu zapiszemy w postaci:

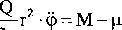
2g

(^{a + b})^r_r

a

Przyspieszenie kątowe krążka w danej chwili wynosi więc: M-a-p.-r(a + b)P

Prędkość kątową uzyskamy, całkując powyższe wyrażenie:

ICąt obrotu krążka jest równy pierwszej całce z prędkości kątowej, czyli:

W powyższych równaniach występują nieznane wielkości (’i, (V leli wartość znajdziemy z warunków początkowych. Przyjmujemy, żc ZHU/.ymimy odmierzać czas od momentu rozpoczęcia hamowania.

Olu t = t₀ =0s , <p = 0, <p ^{= (}»o-Ninie całkowania wynoszą więc:

(a ~    > C₂ — 0 .

«P = 2-g    ₂

r

■i

a • r² ■ Q

(Nalccznie równania opisujące parametry ruchu krążka będą następujące: M-a-p-r(a + b)P

a ■ r² ■ Q M-a-u-r(aH

ip = 2 • g-^-—t + co„

‘l>

M-a-u-r(a + b)P ,

=- 'a' _n ^Lg-^{t +}^-t-

ar Q

K ii|żek zatrzyma się, gdy <p = 0, co nastąpi po czasie t_b czyli: M-a-u-rfa + b)P

() = 2-g-2^--—ti +co₀.

a • r • Q

‘ 111111 obliczamy t_b czyli czas, po którym krążek się zatrzyma:

I    a r² Q «)o

¹    2-g[p-r(a + b)P-M-a]

K i i|żck zatrzyma się, jeżeli ti > 0, czyli:

|ir(a + b)P-M-a>0.

/iim zy to, że jeżeli:

M,

p-r(a + b)

lo umili/,owany układ pozostaje w równowadze statycznej.