mechanika124

Pole grawitacyjne (rys. 3.4)

Na punki materialny poruszający się w przestrzeni działa siła ciężkości (siła potencjalna)    _

G = /ng =»    = -mg, G = P_ae_t    (3-26)

gdzie g =9,81 m/s² przyspieszenie ziemskie (wartość średnia na powierzchni Ziemi).

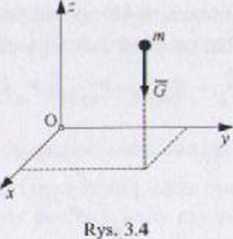
Siła ta jest zawsze skierowana pionowo w dół. Odpowiada jej energiti potencjalna pola grawitacyjnego

E_p{z) = mgz    (3.27)

przy czym poziom zerowy (płaszczyzna xy) jest dowolny.

Pole sprężyste (rys. 3.5)

Jeśli punkt materialny jest połączony z ostoją za pomocą sprężyny pionowe) o sztywności k (N/m), to w przypadku pionowego ruchu tego punktu wystąiu reakcja sprężysta (siła potencjalna)

5 = *|z| P_n « kz => Ś = P^_t    (3.2HI

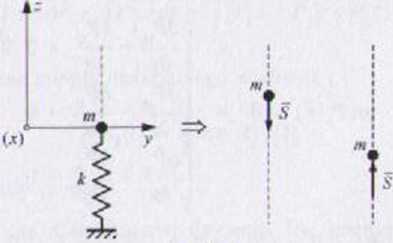
Rys. 3.5

Nil.i ta przeciwstawia się rozciągnięciu lub ściśnięciu więzi sprężystej. Odpo-uuJa jej energia potencjalna (energia sprężysta)

£„U) = jfe²    (3.29)

Uwaga. Sprężyna k i kierunek mchu punktu, mogą być również poziome lub ulośne.

lin erg i a mechaniczna punktu materialnego jest z definicji równa

E(t) = E_k(t)+E_p(t)    (3.30)

Słuszne są następujące twierdzenia odnoszące się do punktu materialnego • polu siłowym potencjalnym.

I sierdzenie 3.7

1'ii a siły potencjalnej w danym przedziale czasu jest równa przyrostowi mrrgii potencjalnej w tym przedziale ze znakiem minus:

L. = -A£„. L, . /P,'dr,    AE„ .£„</„)-E,(«_A>    (3.31)

AD

I sierdzenie 3.8 (zasada równoważności pracy i energii mechanicznej)

h.t« a siły czynnej działającej na punkt materialny w- polu potencjalnym, w danym przedziale czasu, jest równa przyrostowi energii mechanicznej w tym JN/al/iale:

L = AE, A £ = £(r_B)-E(r_A)    (3.32)

I sierdzenie 3.9 (zasada zachowania energii mechanicznej)

■Mli punkt matenalny znajduje się polu potencjalnym i siła czynna jest równa |9tti w danym przedziale czasu, to energia mechaniczna punktu materialnego I tym przedziale jest stała:

£(/) = const => £(r_A) = £(r_B)    (3.33)

I'Mł id/.enie 3.10 (zasada równowagi dynamicznej, zasada d’Alemberta)

I i/dej chwili siły działające na punkt materialny w polu potencjalnym o* i/ i / silą bezwładności £(/) układ zrównoważony

Pyt) - PJf) ⁺ B(t) = 0, Bit) = -ma(t)    (3.34)

iltuinlkn Podtliiwy teoretyczne 249