mechanika143

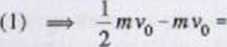
B

0,373<?r„ — - ^ mv₀ = - 0373/ng^    : (- 0,373/ng)

2-0,373mg

=> /„ * 1,340

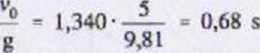
Zadanie 3.16

Blok o masie m porusza się po szorstkiej równi pochyłej. Oprócz siły tarcia ślizgowego, na blok działa siła oporu R = kmv¹ o zwrocie przeciwnym do kierunku ruchu. Współczynnik tarcia ślizgowego kinetycznego bloku o równic wynosi p. Wyznaczyć przemieszczenie x[v), przy warunkach początkowych •*(0) ■ 0, i(0) = v₀. '

V

Dane: m, a. p. k, v_Q Szukane: z(v»)

Rozwiązanie Schemat obliczeniowy:

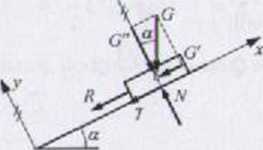
G - mg

G’ = Gsina = mg sin a G" = Gcosa - mg cos a

Siły G\ G" są składowymi ciężaru G w układzie xy.

Układ sił działających na blok traktujemy w przybliżeniu jako plaski zbieżny układ sil. W kierunku y spełnione jest równanie równowagi statycznej:

£ Y = 0: N-G* = 0 =► N = G^m = mgeosa

Siła tarcia ślizgowego: T = \iN • pmgcosa

Równanie ruchu i jego całkowanie:

"«{*) ■ P_s(t)

P_t(t) = -G' - T - R - -mg sin a - pmgcosa - fcmv^?

(I)

286

Dynamika 3.2.2. Dynamika punktu matdijlncgo / wię/amł

(I) «=> rńx = • mg(sino + \i cosa) - kmv²

: m
dv _ V	dv V -
r dr	r ■■■"" dr
	dc

g(sina ♦ m cosa ) + kv'‘

v— = -gtsina *pcosa)-)tv² dr

g(sina - p

l

-1---dv=-dr |/, /

^vo o

^v    i*

- -x ,    x(0) = 0

^r9

ina «• u cosa) ♦ kv^ł    't

In [g(sina ♦ \i cosa) ♦ *v²

c = g(sina ♦ pcosa) — pomocnicza stała I

— In (c + *v²) - In fc ♦ *v₀²)] = - x

•(-1)

x{v) « J- In (c+h>Z) -ln(c ♦ Av²)] » ± ^In —

2* _c ♦ kv

danie 3.17

fr.ścień o masie m przesuwa się bez tarcia wzdłuż pręta AB. pod wpływem ly centralnej P(t), skierowanej do punktu O i odwrotnie proporcjonalnej do “eg {ości pierścienia od punktu O. Współczynnik proporcjonalności wynosi I. W chwili początkowej pierścień jest nieruchomy w położeniu A. Wyzna-yć prędkość pierścienia w położeniu B.

PV)

287

namlktt. t.2 ? Dynamika punktu materialnego / wie/omi