mechanika16

krążek. Zależność między silami P, R nie ulega zmianie, ale siły P i R zamieniają się miejscami (rys. I.38b).

i)    b)

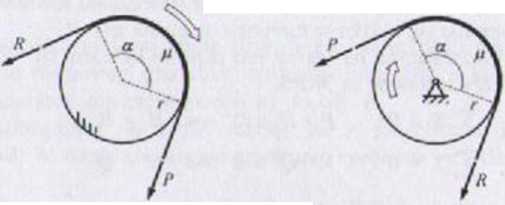
Rys. 1.38

1.1.6. PRZESTRZENNE UKŁADY OBCIĄŻEŃ
Zapis analityczny punktów, siły i	promieni w przestrzeni ma postać (rys. 1.39):
^A(^xa> Za> ^za)	- współrzędne punktu lokacyjnego prostej działania siły P (m].
-^VB’ ^zb)	— współrzędne dowolnego punktu
	(bieguna),
P = Ptet * Pyty + P£ex	— wektor siły.
^pr ^p r	- składowe siły [N], [kN]
^7 m	- promień siły P względem punktu B,
rx=xA-^rB, ry=yA-yB, rt-zA	-zB - składowe promienia 7 (m).
^7o ^m * ^ro>«, * ^roĆz	— promień siły P względem punktu 0.
^rOi ^VA' ^rO> ^= ^A’ ^rOi ~ ^ZK	— składowe promienia rQ [mj.

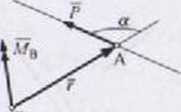
Mdint iii siły względem punktu B jest iloczynem wektorowym (rys. 1.40)

(1.57)

M_b = 7xP

u

H

y

Rys. 1 40

/ definicji iloczynu wektorowego wynika, żc wektor M_Q:

iest prostopadły do płaszczyzny utworzonej przez wektory r, P.

-    ma zwrot zgodny z regułą prawej dłoni.

ma wartość równą polu równoległoboku rozpiętego na wektorach r, P, izn. M_q - rPsina, gdzie a - kąt między wektorami r i P,

-    jesi wektorem zaczepionym w punkcie B, nie zależy od wyboru punktu A na prostej u.

W przestrzeni korzystamy z zapisu wyznacznikowego iloczynu wektorowego:

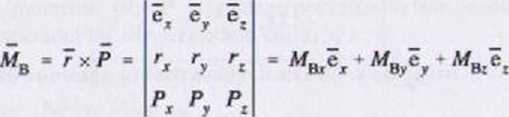
(1.58)

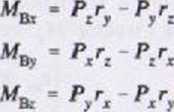
Jednostkami składowych wektora M_B są: [N m], (kN-m]. Wartość momentu M_B wynosi

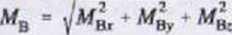
(1.59)

Parą sił nazywamy dwie siły lezące na prostych równoległych, o równych wartościach i przeciwnych zwrotach (rys. 1.41). Moment pary sił jest wektorem

Smyku. Podstawy teoretyczne

32

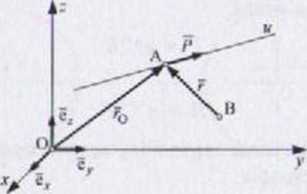
Rys. 1.39

Statyka. Podstawy teoretyczne