mechanika20

Ad 1. Redukcja układu do wypadkowej

Pośredni i końcowy wynik redukcji pokazano na rys. 1.48.

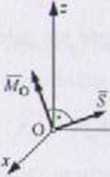
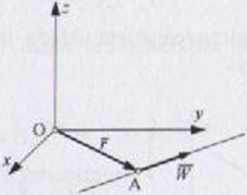
Rys. I.4X

Redukuje poszukiwaną silę W do punktu O. otrzymuje się: 5 = W =* W - W_xl_x + W_yl_y ♦ W,e_t

(1.79)

K-s_x. ^wr^sy>

M_r

rxS = M,

‘o , „    ^ _M „_MQ

W zapisie jawnym równanie wektorowe r x S = Af₀ ma postać

^c* ^ey ^e<

^xa yA Za

S* S, s_z

- M_xe_x ♦ M_ye_y * M_ge_s

(1.80)

Otrzymuje się wówczas nieoznaczony układ równań z niewiadomymi .t_A, y_A, z_A:

V* - Va * ^M«

^Sx«a-Va-^m,    U 81)

k*A Va -

Jedną z niewiadomych przyjmujemy dowolnie. Jeśli S_A * 0. to jedno z rozwiązań ma postać:

M.    Af,

¹ ?a = -«*• *A ' T²    U.82)

⁵jr

Pierwsze równanie jest spełnione tożsamościowe, bo w =0.

Jeśli S. + 0. to można przyjąć y_A 0 i rozwiązać układ.

Jeśli S. * 0. to można przyjąć z_A = 0 i rozwiązać układ

Jest nieskończenie wiele rozwiązań, bo jest nieskończenie wiele punktów A na

prostej u działania wypadkowej (zwanej linią centralną).

40

Statyka. Podstawy icotciycznc

Ad ' Redukcja układu skrętnika

M.jmk jest dowodem jednoznaczności zagadnienia redukcji przestrzennego d<rolnego układu obciążeń. Pośredni i końcowy wynik redukcji przedstawiono nu rys. 1.49. Moment M_Q rozłożono na dwa rzuty: M'_a ± S i M"₀ | S.

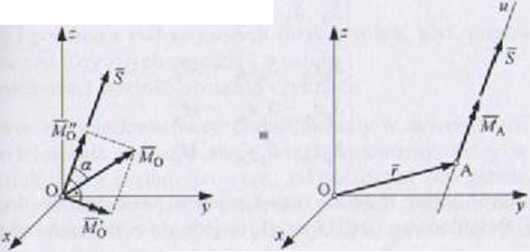
Rys 1.49

Kolincarnc wektory' S, M_A nazywamy skrętnikiem. Wynik nie zalezy od iwsbom punktu A na linii centralnej u. Redukując poszukiwany układ S. M_A do punktu O, otrzymuje się tę samą siłę ogólną, ale o innej prostej działania oraz

M_G = M'₀ +    = 7x5 ♦ M_a =s rx5 = M'₀, M_K = M"₀    (1.83)

Mgorytm obliczeń jest następujący:

- obliczenie wyróżnika układu i kwadratu wartości siły ogólnej

»• = S.jW, - S_yJW_r * S_tM_t.    s² - s; * s² - s²

(1.84)

- obliczenie momentu M_A

c

w S²

* ^MA,^ey '

(1.85)

"a.

M

cS,. M* “ ^cSz

- obliczenie momentu

o

"o - «o - *ó - «₀ - "* - m;s, *

- M,    - ", M_Ał, - M.

(1.86)

Statyka. INulMuwy tcoictyi/nc

dl