mechanika44

(2)    => V_A - P

(3)    => 2//_b= -3P-6P-P-3P => 2H_b * -7P |:2 -+ ff_B =-3.5P (I) => H_a = P ₊ H_b = P-3,5P = -2.5P

Odp.:    //_A    =    -2,5P    (rozciąganie),

V_K    =    P    (ściskanie),

H_h    =    -3,5P    (rozciąganie).

Interpretacja: Założono ściskanie więzów podporowych. W rzeczywistości więzy odpowiadające reakcjom H_K, H_B są rozciągane.

Zadanie 1.35

Wyznaczyć reakcje na podporach ramy:

£ S

| 05 m i 0,5 m

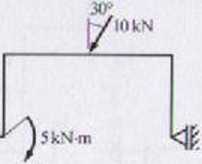
| 0.5 m j 0.5 m |

Rozwiązanie Sprawdzenie GN. SW:

Ramę traktujemy jako jedną tarczę:

Hjl

rr

e = 3, / = l, e = 3t 1 -F GN (1 zasada) GN, SW

Schemat obliczeniowy:

ll

jr
A	B	/\ c
k	K	) M

.4—ł—»-    .* J.    —Ł

b = 0,5 iii 3/ = 5 kN*m

P, - Psin30°= 10* — =5 kN

2

P₂-Pcos30° 10*^| -5^3 kN

SK

Suityka. 1.2.2. Wyznaczanie reakcji w ukl.nl.it h płaskich

0:	^Hc~^p\ = °	(1)
0:	vA + vB-p2 =0	(2)
= 0:	VHb-M + Prb-P23b = 0	(3)
«c	- P, - 5 kN

D) «=► V_Rb = M-P_lb + 3P₂b \:b

K_B =    -P, + 3P₂ ®    -5 + 3*5y3 - 10-5 *25,981 =30,981 kN

b    0,5

(?) => K_A = P, - K_B = 5_v/3 30,981 - 8,660 30,981 = 22,321 kN

Odp.: V_A = -22,321 kN (rozciąganie),

V_Q = 30,981 kN (ściskanie).

H_c = 5 kN    (rozciąganie).

Interpretacja: Przewidziano poprawnie zwroty V_H, H_r. Rzeczywisty zwrot l _v jest przeciwny do założonego na schemacie obliczeniowym.

I 2.3. RÓWNOWAGA GRANICZNA MECHANIZMÓW PŁASKICH Z TARCIEM

/.nianie 1.36 < tato płaskie o ciężarze Q - 2000 N połączono z blokiem o nieznanym ciężarze G za pomocą nieważkiej liny przełożonej przez, krążek nieruchomy. Wyznaczyć ekstremalne wartości ciężaru G. przy których układ jest w równowadze granicznej. Uwzględnić tarcie ślizgowe ciała płaskiego o równię pochy-l.i i tarcie cięgna o krążek.

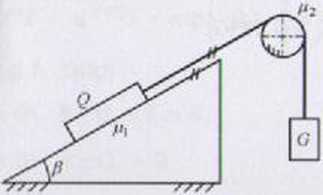
Dane: Q

p, = 0,2 p₂ - 0,1

P = 30° Szukane: G_niln

.89

1KKS:

Statyka. I 2.3 Równowaga graniczna tncchaiu/niów płaskich / tarciem