010 (22)

Zadanie 1 (3p)

Rozwiąż nierówność |x³ -8|<x² + 2x + 4.

Zadanie 2 (6p)

Wyznacz wszystkie wartości parametru m, dla których układ równań \mx-4y- cos²10° + cos² 80° + m \lx + 2y = \

ma dokładnie jedno rozwiązanie spełniające warunki: x>0 i y<0.

Zadanie 3 (4p)

Wielomian -(a-t-ó)*² -(ćj-ó)x + 3 jest podzielny przez wielomian x² _4x + 3 . Oblicz a i b. Zadanie 4 (4p)

Liczbę 2 przedstaw w postaci sumy dwóch takich liczb, by suma sześcianów tych liczb była najmniejsza.

Zadanie 5 (3p)

Sześć osób, dwie panie i czterech panów kupiło bilety na pociąg do tego samego sześcioosobowego przedziału. Numery miejsc były przydzielane w sposób losowy. Oblicz prawdopodobieństwo, że obie panie będą siedziały przy oknie.

Zadanie 6 (6p)

W ostrosłupie prawidłowym czworokątnym kwadrat długości krawędzi podstaw)', kwadrat wysokości i kwadrat długości krawędzi bocznej są kolejnymi wyrazami ciągu arytmetycznego o różnicy 3. Oblicz objętość tego ostrosłupa.

Zadanie 7 (6p)

Za pomocą układu dwóch nierówności opisz zbiór punktów zacieniowany na rysunku.

‘Y

■*>

-i -b

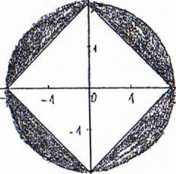
b H

x

Zadanie 8 (3p0

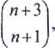
Dane są dwa ciągi (a_n) i (b„). Wyraz ogólny ciągu (a_n) jest określony wzorem a_n =

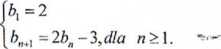
natomiast ciąg (b„) jest określony rekurencyjnie Oblicz a4- Kj.

Arkusz rozszerzony (II - 11)

Zadaniel(3p).

Wyznacz zbiór wszystkich punktów osi liczbowej, których suma odległości od punktów 1 oraz 3 jest mniejsza od 6.

Zadanie 2(3p).

Wyznacz wszystkie wartości x z przedziału <0;2 zr >, dla których liczby cos²x - sin²x ; 0,5sin²x ; 1 - cos²x w podanej kolejności są trzema kolejnymi wyrazami ciągu arytmetycznego.

Zadanie 3(4p).

Dane są punkty A = (2;2), B = (5;3). Na prostej o równaniu x + y = 0 wyznacz punkt C tak, by długość łamanej ACB była najmniejsza.

Zadanie 4(3p).

Z siedmiu osób, wśród których są Janek i Marek, wybieramy losowo trzy osoby. Oblicz prawdopodobieństwo, że w wybranej trójce znajdzie się Marek i nie będzie w niej Janka.

Zadanie 5(4p).

Punkt D jest punktem wewnętrznym trójkąta ABC. Wykaż, że li\AD\ + \BE\ + |C£>|)>|yfJ3| + \BC\ + \AC\

Zadanie 6(6p).

Współczynniki a, b, c wielomianu W(x) = x³ + ax² + bx + c są kolejnymi wyrazami rosnącego ciągu geometrycznego. Reszta z dzielenia tego wielomianu przez dwumian x + 1 jest równia 2, a jego reszta z dzielenia przez x + 2 jest równa -4. Oblicz iloraz ciągu.

Zadanie 7(7p).

Punkty A = (2;7), C = (8; 15) są przeciwległymi wierzchołkami rombu o polu 25. Wyznacz współrzędne pozostałych wierzchołków.

Zadanie 8(5p).

Zbadaj liczbę rozwiązań równania 2jc • (2 - |x|) = m w zależności od parametru m.

Zadanie 9(5p).

Podaj wymiary graniastosłupa prawidłowego czworokątnego o największym polu powierzchni całkowitej, jeżeli suma długości jego wszystkich krawędzi jest równa 6m.

Zadanie 10(5p).

Dane są punkty A = (1 ;4), B = (7; 13). Na prostej AB wyznacz punkt C tak, by |/łC|:|flC| = 2:l.

Zadanie 11 (5p).

Trapez równoramienny o podstawach długości 20 cm i 8 cm oraz kącie ostrym 50°, obraca się dookoła prostej zawierającej dłuższą podstawę. Oblicz objętość powstałej bryły. Wynik podaj z zaokrągleniem do 0,001 cm³.