006 (44)

Przykładowe zadania (poziom rozszerzony):

12.    Wyznacz wszystkie wartości parametru p, dla których równanie |x-2|+|a + 3| = p ma dokładnie dwa rozwiązania.

, . . . -Ja²-6a + 9 \Ja² -4a + 4

13.    Wykaz, ze dla a e (2, j) zachodzi rownosc-+-= 2.

3-o    a-2

14.    Dane jest równanie x² + bx + c = 0 z niewiadomą x. Wyznacz wartości b oraz c tak, by były one rozwiązaniami danego równania.

15.    Dane są funkcje liniowe g i li określone wzorami: g(x) = ax + b i h(x) = bx + a. Wiadomo, że funkcja g jest rosnąca, a funkcja h malejąca.

a)    Wyznacz pierwszą współrzędną punktu przecięcia wykresów tych funkcji.

b)    Oblicz liczby a i b wiedząc, że wykresy funkcji g i h są prostymi prostopadłymi, a punkt ich przecięcia leży na osi Ox.

16.    Dany jest ciąg (a,.) mający tę własność, że dla każdej liczby naturalnej n suma

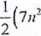
-")■ Oblicz dwudziesty wyraz

n początkowych wyrazów tego ciągu jest równa

tego ciągu. Wykaż, że (a_n) jest ciągiem arytmetycznym.

17.    Proste zawierające ramiona BC i DA trapezu ABCD przecinająsię w punkcie S. Dane są: \AB\ = 6, |CD| = 2 oraz obwód trójkąta SCD równy a/TŚ . Oblicz obwód trójkąta SAB.

18.    W pewnym trapezie kąty pizy dwóch przeciwległych wierzchołkach mają miary a oraz 90 +a. Jedno z ramion tego trapezu ma długość t. Wyznacz różnicę długości podstaw tego trapezu.

19.    Czworokąt ABCD jest wpisany w okrąg. Dane są |5C| = n, |CZ)| = 6, \<DAB\ = a.

Wyznacz długość przekątnej BD.

"— 20. Podstawą ostrosłupa ABCDS jest kwadrat ABCD o boku długości 4. Odcinek DS jest wysokością ostrosłupa i ma długość 6. Punkt M jest środkiem odcinka DS. Oblicz pole przekroju ostrosłupa płaszczyzną BCM.

21. Ze zbioru liczb {1, 2,...,2w + 5} wybieramy jednocześnie dwie liczby. Na ile sposobów możemy to zrobić, tak aby otrzymać dwie liczby takie, że:

a)    ich różnica będzie liczbą parzystą,

b)    suma ich kwadratów będzie liczbą podzielną przez cztery?

Zad.l (4pkt)

gdzie xe (-2,3)u(3,co).

/(*) = ■

W prostokątnym układzie współrzędnych narysuj wykres funkcji: ■\jx² + 4x + 4 yj9-6x + x²

x-3

x + 2 Zad. 2 (4pkt)

W trapez prostokątny można wpisać okrąg. Jedna z jego podstaw ma długość a, druga zaś jest trzy razy dłuższa. Oblicz pole trapezu oraz długość odcinka łączącego środki ramion trapezu. Zad. 3 (5pkt)

2 — x .    .    ,

Funkcja /(x) =-przyjmuje wartości ujemne wtedy i tylko wtedy, gdy

x + b

x e (-oo,-5)u (2,oo).

a)    Oblicz b.

b)    Napisz wzór funkcji f w postaci kanonicznej.

c)    Wyznacz zbiór tych argumentów, dla których funkcja f osiąga wartości niewiększe niż

3x + 8

funkcja g(x) =--.

x + 5

Zad.4 (6pkl)

Trzy liczby, których suma jest równa 93, tworzą ciąg geometryczny. Te same liczby stanowią pierwszy, drugi i siódmy wyraz ciągu arytmetycznego. Wyznacz te liczby.

Zad.5 (5pkt)

Kąt ostry równolegloboku ma miarę 30 . Odległości punktu przecięcia przekątnych równoległoboku od jego boków są odpowiednio równe 2 oraz 6. Oblicz pole równolegloboku i długość jego krótszej przekątnej.

Zad.6 (3pkt)

Dla jakich wartości parametru a, wielomian IV(x) = x³ -(2sin4a)x² + 3x-sin4a-5 jest

podzielny przez dwumian (x-2)?

Zad.7 (5pkt)

Długości boków trójkąta a, b, c (w. podanej kolejności) tworzą ciąg arytmetyczny. Wyraź w procentach, jaką część wysokości trójkąta poprowadzonej na bok długości b stanowi promień okręgu wpisanego w ten trójkąt.

Zad. 8 (6pkt)

a)    Dla jakich wartości parametru m równanie x²+y-2mx+2m-l=0 opisuje okrąg? Podaj współrzędne środka i długość promienia okręgu.

b)    Dla jakich wartości parametru m okrąg ten jest styczny do prostej o równaniu x=4? Zad.9 (5pkt)

W prawidłowym graniastosłupie trójkątnym, pole powierzchni bocznej jest równe sumie pól obu podstaw. Oblicz cosinus kąta a nachylenia przekątnej ściany bocznej do sąsiedniej ściany bocznej.

Zad. 10 (4pkt)

Wielokąt wypukły ma n wierzchołków («>3 i n e N+), spośród których losujemy jednocześnie dwa. Wyznacz n wiedząc, że prawdopodobieństwo wylosowania wierzchołków

wyznaczających przekątną tego wielokąta jest mniejsze od —. Zad.l 1 (3pkt)

Wiadomo, że liczba a jest rozwiązaniem równania — + x = 5, gdzie x&0. Nie wyznaczając

x

a, oblicz wartość wyrażenia — + a³.

a