Photo049

Następnie z tablic rozkładu testu F-Snedecora należy odczytać wartość krytyczną testu F_ar ri, gdzie r, = K +1 = 1, r₂ = T-2(K + l) = 58. Wartość krytyczna testu

wynosi F_005;l;58 = ⁴>⁰¹ - stąd spełniona jest zależność F > F^ ^ , odrzuca się

hipotezę zerową. Stwierdza się, iż badany szereg czasowy zmiennej Y posiada istotne załamanie strukturalne w czerwcu 2003 roku (r = 30).

W kolejnym kroku, w programie Gretl przeprowadzono estymacje KMNK modelu danego wzorem (4.43). Zmienne objaśniające wprowadzone do programu zostały podzielone na dwie części (dwa szeregi czasowe), zgodnie z formułą wzoru (4.43). Punktem podział jest moment załamania strukturalnego - czerwiec 2003. Tablica 5.30 przedstawia taki zbiór danych (patrz również macierz X z przykładu 4.5)

Tablica 5.30

<£ gretl

□018

Plik Narzędzia Sesja Dane Próba imienna Model    Pomo£

skSb.gdt

ID #	Nazwa zmiennej	Pełny opis zmiennej
0	const	stała - automatycznie generowana
m	Y	koszty rodzajowe w firmie A w zł
2	XI	wynagrodzenia w firmie A w zł
3	X1JL	wynagrodzenia do maja 2003, potem 0
4	Xl_2	wynagrodzenia od czerwca 2003, przedtem 0
5	al	stała do maja 2003
6	a2	stała od czerwca 2003
7	tl	zmienna czasowa do maja 2003, potem 0
8	t2	zmienna czasowa od czerwca 2003, przedtem 0

Miesięczne: Pełny zakres 2001:01 - 2005:12

jal^InlEglltelfflklLd fi lal

Źródło: Opracowanie własne.

Model dany wzorem (4.42), oszacowany w programie Gretl przedstawia tablica 5.31, model ten można zapisać w postaci:

y, =50435,7+ 73659,4+1,2U,„ + 0,62x_l2l +1600,13/, + 598,14r₂.

(10457.3)    (49834.2)    (0.10)    (0.63)    (273.62)    (316.46)

Współczynnik determinacji R~ =0,895102, wskazuje na wysoki stopień dopasowania modelu do danych empirycznych (tablica 5.32, wykres dopasowania). Statystyka DW = 1,87745 sugeruje brak autokorelacji I rzędu składnika losowego (rozdział 4.3.3.).

Tablica 5.31

_r prfycta lesty Wykresy Qane nxdokj

jiodel 1: Estymacja KMNK 2 wykorzystaniem 60 obserwacji 2001:01-2005:12 2»ienna zależna: Yi

Zmienna

Współczynnik Błąd stand. Statystyka t Wartość p

al	50435,7	10457,3	4,823	0,00001	***
a2	73659,4	49834,2	1,478	0,14519
XI 1	1,20657	0,0968604	12,457	<0,00001	***
XI 2	0,619328	0,631792	0,980	0,33132
tl	1600,13	273,616	5,848	<0,00001	***
t2	598,140	316,458	1,890	0,06412	*

Średnia arytmetyczna zmiennej zależnej = 164552

Odchylenie standardowe zmiennej zależnej = 36412,3

Suma kwadratów reszt = 8,20571e+009

Błąd standardowy reszt » 12327,1

Wsp. determinacji R-kwadrat = 0,895102

Skorygowany wsp. R-kwadrat = 0,885389

Statystyka F (6, 54) = 1858,71 (wartość p < 0,00001)

Statystyka testu Durbina-Watsona ■ 1,87745

Autokorelacja reszt rzędu pierwszego = 0,0374882

Logarytm wiarygodności » -647,149

Kryterium informacyjne Akaika (AIC) = 1306,3

Kryterium bayesowskie Schwarza (BIC) = 1318,86

Kryterium infor.Hannana-Quinna (H<2C) = 1311,21

Zamknij

Iło: Opracowanie własne.

Tablica 5.32

V gretl: wykres gnuplot    □055

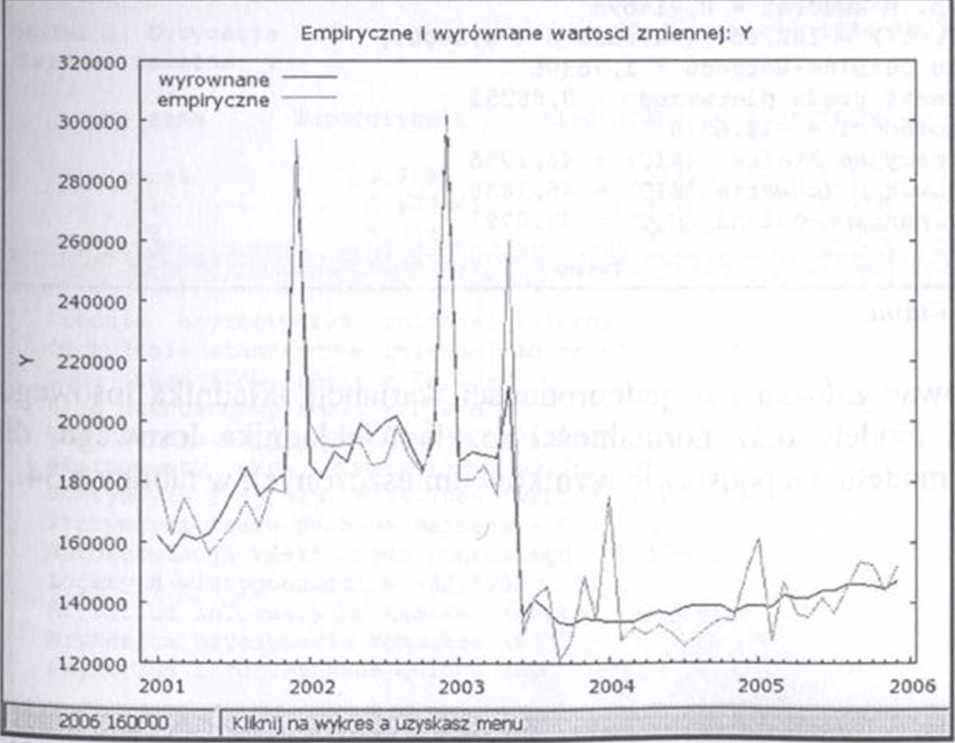
Źródło: Opracowanie własne.

141