przykładowe zadania z matematyki na egzamin

2009 r.

Przykładowe zadania na egzamin z matematyki II (po II semestrze)

dla kierunku budownictwo

1. Za pomocą twierdzenia, de 1’Hospitala wyznaczyć niektóre granice, np:

lim

x-^rc

2 + 2 cos x + sin x

sin 2x

2. Napisać równanie stycznej i normalnej do danej krzywej w punkcie P, np:

y

= x³ + x -3,    P=(l,l).

3. a) Jakie asymptoty ma funkcja y

_ 2x² x-3

9

9    9

b) Podać przykład funkcji, która ma asymptotę poziomą y = 3 i asymptotę pionową x = 2.

4.    Wyznaczyć ekstrema lokalne funkcji: a) y =    _?    ^b) y = (x + 3)e^2x itp. Wykonać

bez szczegółowego badania szkic wykresu funkcj i z przykładu (b).

5.    Określić wartość najmniejszą i największą funkcji y = x-3x² + 3 w przedziale <-l;3> Naszkicować wykres tej funkcji w podanym przedziale.

6. Wyznaczyć dziedzinę funkcji 2 zmiennych z -

_ y

x²+y

7.    Sprawdzenie umiejętności obliczania pochodnych cząstkowych.

Dla funkcji 2 zmiennych z = ~= + x² lny określić grad z(4, 1) oraz określić wartość

•Jx

różniczki dz w punkcie (4,1), przyjmując Ax = 0,01; Ay = 0,02.

8.    Wyznaczyć ekstrema lokalne funkcji 2 zmiennych (wg zadań z listy), np. dla funkcji z = x³ - 6xy + 3Y² + 1.

9. Wyznaczyć niektóre całki nieoznaczone (wg zadań z listy dotyczących całkowania funkcji elementarnych, całkowania przez podstawianie i przez części oraz całek funkcji wymiernych,

^np‘ I(x-3)(x+l)^^

Niektóre całki funkcji niewymiernych obliczane przy użyciu tablicy całek.

10. a) Obliczanie całek oznaczonych;

b)    Obliczyć pole powierzchni obszaru ograniczonego podanymi liniami, np. liniami y =x,

y = l/x, x = 3.

c)    Obliczyć objętość bryły obrotowej, otrzymanej przez obrót wokół osi Ox obszaru ograniczonego danymi liniami, np. liniami y = 0, y = 1 - x .

7    oo

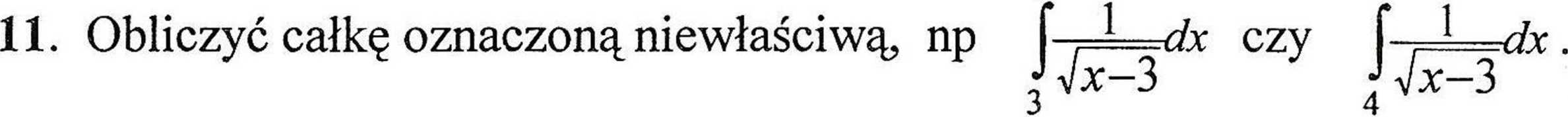
J. Szymczak