skanowanie0040 2

88 Mechanika

skrzypce, ludzkie struny głosowe), drgające stupy powietrza (np. piszczałki organy, klarnet) oraz drgające płyty i membrany (np. bęben, głośnik). Te drga; jące przedmioty na przemian zagęszczają i rozrzedzają otaczające powietrze, po-j wodując ruch cząsteczek do przodu i do tyłu. Powietrze przenosi to zaburzenie oa źródła w przestrzeń.

Wrażenie odbieranego dźwięku jest określone przez jego natężenie, wy.ro; kość i barwę. Wymienione cechy dźwięku zależą od odpowiednich parametrów falowych - amplitudy, częstotliwości oraz zawartości drgań harmonicznych.

Prędkość fali w powietrzu

Ogólne wyrażenie określające prędkość rozchodzenia się fal podłużnych w ośrodku ciągłym ma postać:

(22.6);

E

^V = J-’

\P

gdzie: E oznacza moduł Younga ośrodka, p-jego gęstość.

Przekształcając podstawową postać prawa Hooke’a (patrz rozdz. 18), możemy napisać:

E = —

dp

clV IV

(22.7)

gdzie dp i dV oznaczają odpowiednio różniczkowe zmiany ciśnienia i objętością gazu o objętości V.

Drgania dźwiękowe zachodzą tak szybko, że ściskanie i rozrzedzanie gazu można uważać za procesy adiabatyczne, wobec czego zmiana stanu gazu zachodzi zgodnie ze wzorem Poissona

pV^K = const,    (22.8)

gdzie rjest stosunkiem ciepła właściwego przy stałym ciśnieniu do ciepła właściwego przy stałej objętości- (dla gazów 2-atomowych tc= 1,4).

Po zróżniczkowaniu wzoru Poissona otrzymujemy:

V^Kdp + W^K-'pdV = O,

a stąd

(22.9)

dp

dV IV

Po podstawieniu uzyskanej wartości do równania (22.7), a następnie uwzględnieniu otrzymanej w ten sposób postaci modułu Younga w równaniu (22.6) wyrażamy prędkość fali podłużnej wzorem:

Aby wyeliminować gęstość p, bierzemy definicję tej wielkości i mnożymy licznik i

mianownik przezp - ciśnienie gazu. Zauważamy, że w mianowniku mamy iloczyn pV, który możemy zastąpić iloczynem nRT na podstawie równania stanu gazu:

(22.11)

m p _ mp

V p nRT ’ gdzie: m - masa gazu, n - liczba moli gazu, R - stała gazowa, T-temperatura.

Liczbę moli n można wyrazić jako stosunek całej masy gazu m do masy 1 mola u: n = ni/p. Uwzględniwszy powyższe w równaniu (22.11), wstawiamy wartość p do równania (22.10) i otrzymujemy wzór na prędkość dźwięku w zależności od rodzaju gazu i temperatury:

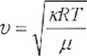
(22.12)

Zasada pomiaru

Celem ćwiczenia jest wyznaczenie prędkości dźwięku V w powietrzu na pod stawie związku

(22.13)

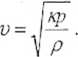
v = Xf ,

gdzie X jest długością fali, a/- częstotliwością.

Częstotliwość jest mierzona bezpośrednio miernikiem, natomiast do wyznaczenia długości fali zastosujemy metodę objaśnioną poniżej.

Na jednym z końców poziomej ławy ustawiamy głośnik połączony z generatorem drgań elektrycznych pełniący funkcję źródła fal (rys. 22.2). Do ich odbioru używamy mikrofonu przesuwanego na ruchomym wózku wzdłuż ławy.

Napięcie głośnika przykładamy do płytek X oscyloskopu, a napięcie z mikrofonu podajemy na płytki Y. Oba napięcia są zmienne w czasie i odzwierciedlają ruch drgający cząsteczek powietrza. Na ekranie oscyloskopu otrzymamy obraz w postaci tzw. figur Lissajous (rys. 22.3).

Figura Lissajous jest wynikiem nałożenia się dwóch ruchów harmonicznych, których kierunki drgań są względem siebie prostopadle. Jej kształt zależy od różnicy faz drgań składowych oraz od stosunku ich częstotliwości. W naszym ćwiczeniu częstotliwość obu drgań jest równa, więc o kształcie figur Lissajous decyduje różnica faz głośnika i mikrofonu. Jeżeli przyjmiemy położenie głośnika x - 0 , to faza jego drgań <p_K w pewnej chwili f, zgodnie z równaniem (22.2), wynosi cot + <y_c. W tej samej chwili do mikrofonu dochodzi fala wytworzona przez odpowiednio wcześniejsze drganie głośnika. Drgania mikrofonu oddalonego od głośnika o ,v