skan0031

76

rozwiązanie to zapiszemy następująco

1/(0 = w	T 1 1	+ G2 (cos t + isint)		-i 1	+ Ga (cos /. — ?! sin /.)		'-1 i 1
= Cie^1	'1' 1	+	-(G2 + C3)cost + i( (Ci + G3) sini + i(—		—Ci + C3)sint Ci + G3) cos t

1    (Ci + m) cos t + t(C2 - Cs) sin t

Cie*	m 1	tó(G2 + G3)	cos t — sin t	+ (—Ci + Cz)i	sin t cos t
	1		— cos t		— sin t

= £>ie*	1' 1	+ Di	cos t — sini	+ D$	sin t cos t
	1		— cost		— sin t m

gdzie D\ = Ci, D2 ^{= —}G2 — G3, Dz^f(—Ci + C3)*.

2.10.1. Przypadek wielokrotnych wartości własnych

Niech A będzie wartością własną o wielokrotności k > 1. W przypadku gdy dla danej wartości własnej A liczba liniowo niezależnych wektorów własnych jest) mniejsza niż k, należy postąpić inaczej niż w poprzednich zadaniach. Omówimy ten przypadek jedynie dla k = 2. Załóżmy więc, że mamy tylko jeden wektor własny! dla wartości własnej A o wielokrotności k = 2, czyli mamy jedno rozwiązanie!

ui = a?⁽1)e^At

równania wektorowego (2.10.4). Drugiego rozwiązania równania (2.10.4) szukamy w postaci

u₂ - x⁽¹he^xt + we^xt.    (2.10.5)

Podstawiając to wyrażenie do równania (2.10.4), otrzymamy równość

_xMe^xt + Xx^he^xt + Aive^xt = Ax^te^Xt + Awe^xt.    (2.10.6)

Przyrównując współczynniki przy te^xt i e^Xi, otrzymamy dwa równania Xx^ = Ax(¹\*

I wlii)|(l, wynika, że

(A - flfpl = O, ^W(A - \I)w =    (2.10.7)

Bftu ważmy, że wektory a^^{1 2}' i w muszą spełniać dwa ostatnie równania. Pierwsze Bwnanil oznacza, że jest wektorem własnym dla wartości własnej A. Znając ■W, należy z drugiego równia wyznaczyć w.

Wyznaczyć rozwiązania następujących zagadnień początkowych:

1. y'(t) =

1 1 0 1

mm y(o) =

2. y'{t) = Ay{t), 2/(0) =

2’		2	1	0'
—1	, A =	0	-3	ii
3		-1	-13	4

1

0

1

1

mamy

l i-A 1 0    1-A

(1 — A)²,

czyli Ai = A2 = 1 są wartościami własnymi macierzy A. Liczba 1 jest podwójną wartością własną macierzy A. Szukamy wektorów własnych dla Ai,2 = 1, a więc z układu równań

0 1:0 .0 0 : OJ ’

otrzymamy

wm

a		T
0	= Ot	0

Zauważmy, że wyznaczyliśmy tylko jeden liniowo niezależny wektor własny, a musimy mieć dwa liniowo niezależne rozwiązania. Jedno rozwiązanie jest dane

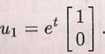
wzorem

Znając wektor własny X'²! i wartość własną A = 1, wyznaczymy wektor w z drugiego równania z (2.10.7). Równanie to przyjmie postać

1 : 1 0 I 0

0

1

II o/, wiązania

2

Zauważmy, że dla