SPá095

Przyk┼éadowe zadania z matematyki dotycz─ůce egzaminu / I semestru na kierunku

budownictwo
x + 2v + z = ÔÇö 1
1. Metod─ů eliminacji rozwi─ůza─ç uk┼éad r├│wna┼ä
[3x-y + 2z = 2
rownan równań np
2. Zadania dotycz─ůce dzia┼éa┼ä na wektorach oraz wyznaczanie r├│wnania p┼éaszczyzny w przestrzeni K i n-Hi-ni┼ä prostej w przestrzeni R. a tak┼╝e r├│┼╝nych postaci prostej na p┼éaszczy┼║nie R . Znajomo┼Ť─ç tych
vnan.
. a) okre┼Ťli─ç odleg┼éo┼Ť─ç punktu P = (2. 3) od prostej y = 2x - 5:
rx = 2 + t
x = 2 - 3t
i 12: "j y = 1 +1 w przestrzeni R:'
z = 3, t e R
y = 1 - 2t z = 3 + 2t, t e R
bl pod jakim k─ůtem przecinaj─ů si─Ö proste 1,: -j
(sk─ůd wiadomo, ┼╝e si─Ö przecinaj─ů?) c i wyznaczy─ç punkt wsp├│lny prostej 1, i p┼éaszczyzny 2x - y +z =0; d czy prosta 1;. jest r├│wnoleg┼éa do p┼éaszczyzny x + 3y +2z = 0 czy nie ?
3. Naszkicowa─ç wykres funkcji: y = ,v2 - 4.v| y = >'-2 + 3
y=llog2-v|,
4 A yZnaczy─ç dziedzin─Ö funkcji: f(x) =
y = |.v| + 2.v itp.
/(ÔÇóv) = log(.v~ -1)
5 Okre┼Ťli─ç funkcje odwrotne do funkcji y = 2 VÔÇťÔÇť b. Upro┼Ťci─ç wyra┼╝enie: aresinj ÔÇö j ÔÇŁÔľá ÔÇÖ-v}7naczy─ç dane Crroni--
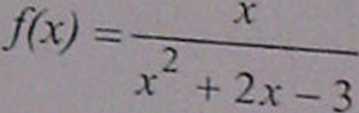
itp.
+ arccos
ÔÇÖ y = I┬░g2(-V + 3), y = J* -arc,g(V3) itp.
-v-3
Inn ~_z.
lim -ii_ *~>2+ x - 2
CJi:
lim
Ôľár~>3o
3.t
.V - Ôľá)
itp.
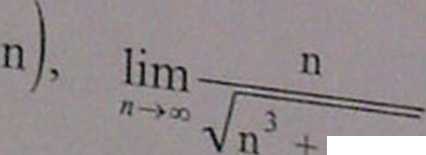
n - 1

- £
Wyszukiwarka
Podobne podstrony:
Pytania - zagadnienia na egzamin dyplomowy na kierunku Budownictwo - 1 stopień studiów - studia
Pytania - zagadnienia na egzamin dyplomowy na kierunku Budownictwo -1 stopień studiów studia st
egzamin dyplomowy na kierunku Budown -1 stopień studiów 2/7 K-62 Katedra Fizyki Budowli i Materiałów
3/7 egzamin dyplomowy na kierunku Budownictwo -1 stopień studiówK-63 Katedra Mechaniki Konstrukcji (
4/7 egzamin dyplomowy na kierunku Budownictwo -1 stopień studiówK-63 Katedra Mechaniki Konstrukcji (
5/7 egzamin dyplomowy na kierunku Budownictwo -1 stopień studiów(K-65) Katedra Budownictwa Betonoweg
6/7 egzamin dyplomowy na kierunku Budownictwo -1 stopień studiów(K-66) Katedra Geotechniki i Budowli
7/7 egzamin dyplomowy na kierunku Budownictwo -1 stopień studiów(K-66) Katedra Geotechniki i Budowli
przykładowe zadania z matematyki na egzamin 2009 r. Przykładowe zadania na egzamin z matematyki II (
informator ezaminacyjny009 Etap pisemny egzaminu Przykładowe zadanie 2. Jak nazywa się przedstawio
Przysiadowe zadania z rozwi─ůzaniami: poziom podstawowy 41 4. Przyk┼éadowe zadania z matematyki na poz
Przykład Zadanie Przetwarzanie iteracyjne kolekcji Operacje na kolekcjach (iterable) Implementacja
Przyk┼éadowe zadania z j─Özyka polskiego Cz─Ö┼Ť─ç pisemna na poziomie podstawowym 1. Testy Zestaw 2. Jan
PRZYKŁADOWE ZADANIA Z MATEMATYKI Https://ma&i275.6 Co cj spot. 7. Oblicz. a) 100 -21
PRZYKŁADOWE ZADANIA Z MATEMATYKI Https: //ma(a275.6Cogspot.com 54. Porówna] liczby. Wpisz w miejsce
Technik budownictwa wodnego - errata - sierpie┼ä 2011 Przyk┼éadowe zadanie 30. Je┼╝eli roboty polegaj─ůc
od semestru letniego 2011/2012Zestaw pytań na egzamin magisterski na kierunku
wi─Öcej podobnych podstron