0055

56

I. Teoria granic

którego licznik jest sumą wszystkich liczników napisanych powyżej ułamków, a mianownik jest sumą wszystkich mianowników. Tak więc przy n>N jest

i^-yw

Napiszmy teraz tożsamość (łatwą do bezpośredniego sprawdzenia)

skąd

x* _t_x_N-ly_N | / /x„-x_N \

y. y» \ w Ih-y# /’

xn — (ywl |-*i>—x_K    J

y*

\y»—yn

Drugi składnik po prawej stronie nierówności staje się przy n>N mniejszy od ie, jak to widzieliśmy wyżej. Pierwszy składnik, ze względu na to, że y„-» + oo, również będzie mniejszy od je np. przy n>N'. Jeśli przy tym obierzemy N’>N, to dla n>N' mamy oczywiście

<«,

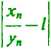
co dowodzi naszego twierdzenia.

Przypadek granicy nieskończonej sprowadza się do przypadku już rozważonego. Niech np.

,. x_n x_n—i

lim-= + co .

y*-y«-1

Wynika stąd przede wszystkim, że (dla dostatecznie dużych n)

x*-x„-i>y,-y_n-i,

skąd otrzymujemy, że wraz z {y„} również i {x„} dąży do +co, przy czym wartości ciągu {*„} rosną wraz ze wzrostem n. W tym przypadku udowodnione twierdzenie można zastosować do odwrotności ilorazu yjx_n:

hm —=hm--=0

x„-x„.₁

(bo tu ta granica jest już skończona), skąd już wynika, że lim xjy„= +°o, cnd. Przejdźmy znowu do przykładów.

12) Widzieliśmy już w przykładzie 9), że przy a> 1

lim —= + oo . n

Wynik ten za pomocą twierdzenia Stolza otrzymujemy od razu:

lim— = lim {a—a ¹) = lima" n

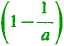
= -|-oo.

Ta sama uwaga odnosi się do przykładu 11).

13) Zastosujemy twierdzenie Stolza do dowodu interesującego twierdzenia Cauchy’ego: Jeżeli ciąg {a„} ma granicę (skończoną lub nieskończoną), to tę samą granicę ma również ciąg

tfi+<?2+ ■■•+a«i

{średnia arytmetyczna pierwszych n wartości ciągu {a,}.