0064

(6)

(6)

65

1

§ 3. Ciąg monotoniczny

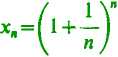
¹ n(n-l) 1 n(n —l)(n—2)    1

^l+"7⁺TTV-⁺“m^_'»'^ił

n(n —l)...(n —fc + 1) 1    n(n —l)...(n — n + 1)

⁺ -⁺ I -2*... - A:    IT* ⁺ "' ⁺-12 ... „-

= 1 + 1 +

iKK('4)K)* *

*M'+)

Jeżeli od x_n przejdziemy teraz do jc_a+1, tj. zwiększymy n o jedność, to przede wszystkim pojawi się nowy (n+2)-gi (dodatni) wyraz, a każdy z już napisanych wyrazów się zwiększy,

s

bo dowolny czynnik w nawiasach postaci 1— zastępujemy większym czynnikiem

n

s

1--. Wynika stąd, że

n+1

tj. ciąg {*„} jest ciągiem rosnącym.

Pokażemy teraz, że ciąg ten jest także ograniczony z góry. Opuszczając w wyrażeniu (6) wszystkie czynniki w nawiasach, powiększamy je, czyli

1 1 1

Zastępując dalej każdy czynnik w mianownikach ułamka (rozpoczynając od trzeciego) liczbą 2, jeszcze bardziej zwiększamy otrzymane wyrażenie, tak że

1 1 1

y«^<2+Y+^2⁺—⁺2^i •

Ale postęp (zaczynający się liczbą |) ma sumę mniejszą niż 1, a więc x_n<y„<3.

Stąd już wynika, na podstawie twierdzenia z ustępu 34, że ciąg {*„} ma granicę skończoną. Za przykładem Eulera, oznaczamy ją literą e. Liczba ta

ma wyjątkową wagę zarówno w samej analizie, jak w jej zastosowaniach. Podajemy pierwsze 15 cyfr jej rozwinięcia w ułamek dziesiętny

e=2, 71828 18284 59045...

W następnym ustępie pokażemy przykład obliczania przybliżonego liczby e, a także ustalimy po drodze, że e jest liczbą niewymierną.

Pewne własności liczby e, które ustalimy później [54 (13)], czynią szczególnie wygodnym wybór tej właśnie liczby za podstawę układu logarytmów. Logarytmy przy podstawie e

5 G. M. Fichtcnholz