Untitled 22

36J

§ 3. Ciąg monotoniczny

65

(6) x„ = [ 1+—^ =l+n

1 n(n-1)    1 n(n — l)(n—2)    1

1-2 n'

1-2-3

n(n— 1)...(« — k+ 1)    1    n(n — l)...(n — n +1)    1

\ -2 -... ■ k n*⁺"' ⁺ T-2■... -n n*

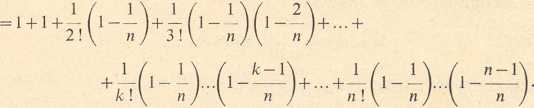
Jeżeli od x_n przejdziemy teraz do x_n+l, tj. zwiększymy n o jedność, to przede wszystkim pojawi się nowy (« + 2)-gi (dodatni) wyraz, a każdy z już napisanych wyrazów się zwiększy,

bo dowolny czynnik w nawiasach postaci 1 — zastępujemy większym czynnikiem

n

s

1--. Wynika stąd, że

n+ 1

tj. ciąg {*„} jest ciągiem rosnącym.

Pokażemy teraz, że ciąg ten jest także ograniczony z góry. Opuszczając w wyrażeniu (6) wszystkie czynniki w nawiasach, powiększamy je, czyli

„ ¹ 1 1

< 2    -ł—-=y„.

2 ! 3 ! n !

Zastępując dalej każdy czynnik w mianownikach ułamka (rozpoczynając od trzeciego) liczbą 2, jeszcze bardziej zwiększamy otrzymane wyrażenie, tak że

1 1 1

^<2+— +-₂ + .--+—i •

1

Ale postęp (zaczynający się liczbą |) ma sumę mniejszą niż l, a więc x_n<y_n<3.

Stąd już wynika, na podstawie twierdzenia z ustępu 34, że ciąg {x„} ma granicę skończoną. Za przykładem Eulera, oznaczamy ją literą e. Liczba ta

ma wyjątkową wagę zarówno w samej analizie, jak w jej zastosowaniach. Podajemy pierwsze 15 cyfr jej rozwinięcia w ułamek dziesiętny

e — 2, 71828 18284 59045 ...

W następnym ustępie pokażemy przykład obliczania przybliżonego liczby e, a także ustalimy po drodze, że e jest liczbą niewymierną.

Pewne własności liczby e, które ustalimy później [54 (13)], czynią szczególnie wygodnym wybór tej właśnie liczby za podstawę układu logarytmów. Logarytmy przy podstawie e

5 G. M. Fichtenholz