0183

184

III. Pochodne i różniczki

104. Związek między różniczkowalnością a istnieniem pochodnej. Łatwo jest ustalić teraz słuszność następującego twierdzenia:

Na to, żeby funkcja y=f(x) była różniczkowalna w punkcie x₀, potrzeba i wystarcza, by miała ona w tym punkcie pochodną skończoną y'=f'(x₀). Jeśli warunek ten jest spełniony, to równość (1) zachodzi dla wartości stałej A równej tej pochodnej

(la)    Ay = y'_xAx + o(Ax).

Konieczność. Jeśli spełniony jest warunek (1), to

Ay    o(Ax)

— = A-i--,

Ax    Ax

tak że przy Ax~*0 otrzymujemy rzeczywiście

. .. dy , zł = hm —=y_x. a_x^oAx

Dostateczność wynika od razu z ustępu 96, 1° (patrz wzór (3a)).

Tak więc różniczka funkcji y=f (x) równa się zawsze

(2)    dy=y'_xAx(¹).

Podkreślimy tu jeszcze, że przez Ax rozumiemy w tym wyrażeniu dowolny przyrósł zmiennej niezależnej, tj. dowolną liczbę (którą często wygodnie jest uważać za niezależną

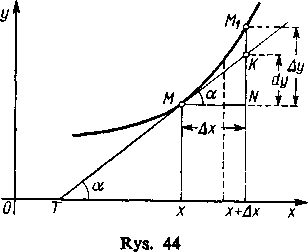
od jc). Nie musimy wcale przy tym uważać, że Ax jest nieskończenie mała; lecz jeśli Ax->0, to różniczka dy również będzie nieskończenie mała, a mianowicie (gdy y^O) będzie częścią główną nieskończenie małego przyrostu funkcji Ay. To właśnie pozwala nam przyjmować w przybliżeniu

(3)    Aywdy

z tym większym stopniem dokładności, im mniejsze jest Ax. Powrócimy do rozpatrzenia równości przybliżonej (3) w ustępie 107.

Aby dać geometryczną interpretację różniczki dy i związku jej z przyrostem Ay funkcji >’=/(x), rozpatrzymy wykres tej funkcji (rys. 44). Wartość x argumentu i wartość y funkcji wyznacza punkt M na krzywej. Poprowadźmy przez ten punkt krzywej styczną MT\ jak już widzieliśmy [92], jej współczynnik kątowy tg a jest równy pochodnej y_x. Jeśli nadamy odciętej x przyrost Ax, to rzędna na krzywej

O Łatwo jest sprawdzić, że tak właśnie obliczaliśmy różniczkę we wszystkich przypadkach rozpatrywanych w poprzednim ustępie. W przypadku ł) mamy na przykład

Q=nr², Q'_r=2nr, dQ=2nrAr itd.