0469

470

VII. Zastosowania rachunku różniczkowego do geometrii

Jeżeli się połączy (rys. 119 na str. 454) punkt D z M, to prosta ta utworzy z osią x kąt

$.xTD= %DOT+ *OD 7 = mt+\t.

Zatem prosta DT jest styczną w punkcie M, a MB — normalną.

6) Ewolwenta kola x-a(t sin /+cos t), _r = atsin t — t cos t) (rys. 121 na str. 456). Tutaj

tga=—=tg/, skąd <x=t. x_t

Tym samym styczna MTjest równoległa do promienia OB, i BM jest normalną do krzywej.

Uwaga. Wyniki z przykładów 4), 5) i 6) można byłoby otrzymać bez żadnych rachunków z rozważań kinematycznych. Przy toczeniu jednej krzywej po drugiej punkt styczności jest zawsze chwilowym środkiem obrotu dla toczącej się krzywej, a więc normalna do trajektorii dowolnego punktu tej krzywej musi przechodzić przez punkt styczności.

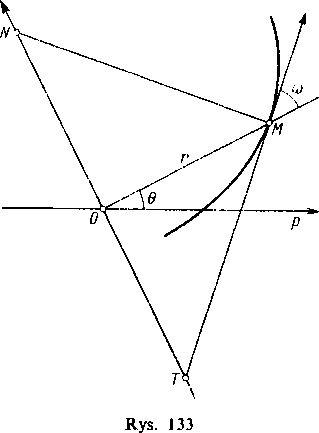
232. Styczna we współrzędnych biegunowych. Jeżeli krzywa dana jest równaniem biegunowym r=f(6), to przechodząc w zwykły sposób do współrzędnych prostokątnych otrzymujemy jej przedstawienie parametryczne w postaci

x — rcosO=f(0) cos0, y = rńnO=f(Q) sin0,

przy czym rolę parametru gra 9.

W przypadku tym otrzymujemy z ogólnego wzoru (6)

v« r'_e sin0+r cosO

tg a =¹— =-■

x'_e rgCos8 — rsin9

Jeżeli jednak krzywą rozpatruje się we współrzędnych biegunowych, to położenie stycznej określa się zazwyczaj nie kątem a z osią biegunową, lecz kątem co z przedłużeniem promienia wodzącego (rys. 114 na str. 433 oraz rys.

133). Znamy już [218, 4)] prosty wzór

(8)    tg co = —~ •

r_e

Podobnie, zamiast odcinków t, n, podstycznej i podnonnalnej, o których mówiliśmy w ustępie 230, rozpatruje się tutaj inne odcinki. Mianowicie, poprowadźmy przez biegun O oś prostopadłą do promienia wodzącego (oś ta obraca się przy zmianie położenia punktu M) i przedłużmy styczną i normalną do przecięcia się z tą osią odpowiednio w punktach T i N. Odcinki TM i MN nazywamy odcinkami biegunowymi stycznej i normalnej, a ich rzuty TO i ON na poprowadzoną oś nazywamy podstyczną biegunową i podnormalną biegunową. Odcinki te będziemy oznaczali tak jak poprzednio pisząc tylko u dołu wskaźnik p. Korzy-