0499

500

VII. Zastosowania rachunku różniczkowego do geometrii

Jeżeli S jest liczbą skończoną, to krzywą nazywamy prostowalną lub rektyfikowa-

InąC).

Z definicji długości krzywej wynika, że długość dowolnej łamanej wpisanej w krzywą AB nie przekracza długości S krzywej; w szczególności dotyczy to długości cięciwy AB łączącej punkt początkowy krzywej z punktem końcowym.

Weźmy teraz na krzywej AB punkt C między A i B, a więc punkt odpowiadający wartości t=t* zawartej między t₀ a T (t₀<t*<T).

Jeżeli krzywa AB jest prostowalna, to prostowalny jest każdy z luków AC i CB. Na odwrót, z prostowalności tych luków wynika prostowalność całej krzywej AB. Oznaczając długości luków AB, AC i CB odpowiednio przez S, S' i S” mamy przy tym równość

(4)    S=S’ + S".

Dla dowodu załóżmy najpierw, że krzywa AB jest prostowalna i wpiszmy dowolne łamane o długościach p' i p" odpowiednio w łuki AC i CB. Łamane te razem wzięte tworzą łamaną o długości

P'+P"=P

wpisaną w krzywą AB. Ponieważ p^S, czyli

(5)    p'+p"śS,

jest oczywiście p'^S oraz p"^S. Tym samym zbiory {p'} i {p") są ograniczone z góry (5 jest skończone!) i łuki AC i CB są prostowalne, bo mają skończone długości

S' = sup {p'},    S"=sup{p"}.

Z własności kresu górnego [11] wynika, że każda z długości p' i p" niezależnie, może być dowolnie bliska swego kresu - odpowiednio S' i S".

Zatem z nierówności (5) przez przejście graniczne otrzymujemy

(6)    S'+S"^S.

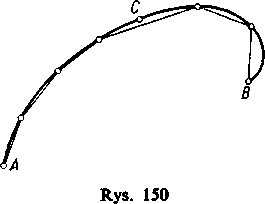
Przypuśćmy teraz, że wiemy, że łuki AC i CB są prostowalne i wpiszmy dowolną łamaną o długości p w krzywą AB. Jeżeli punkt C jest jednym z jej wierzchołków, to rozpada się ona na dwie łamane o długościach p’ i p" wpisane odpowiednio w łuki AC i CB. Jeżeli zaś punkt C nie jest jej wierzchołkiem, to dołączmy go do wierzchołków — długość łamanej może się przez to tylko zwiększyć (rys. 150). Nowa łamana rozpada się jak poprzednio na dwie. W obu przypadkach jest

P<p' + p"<S' + S".

O Zwracamy uwagę czytelnika na wagę sprecyzowania pojęć zwrotu na krzywej oraz łamanej wpisanej. Jeśliby punkty M, mogły być obierane dowolnie, to kres górny S równałby się zawsze +oo.