0451

452

do postaci

VII.. Zastosowania rachunku różniczkowego do geometrii

, 2 .    2    2s3 .    2 2    2 _n

(x +y —a ) -rlla x y =0.

Przy tym przedstawieniu wymienione punkty są właśnie osobliwe.

Z równania krzywej widać, że leży ona w kole x²+y²=a² i jest symetryczna względem osi współrzędnych. Wobec tego ograniczymy się do pierwszej ćwiartki układu współrzędnych. Rozwiązując równanie względem y:

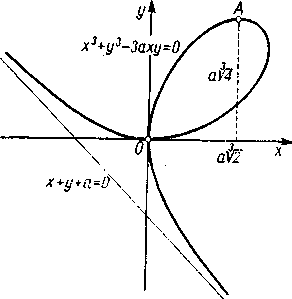
Rys. 117

y—(.a^2l3—x^2l3)^3>2 i obliczając pochodną

y' = —(a —x ) x ,

widzimy, że dla x — 0 styczna jest pionowa, a dla x~a — pozioma. Wynika stąd, że we wszystkich czterech punktach osobliwych krzywa ma ostrza (punkty zwrotu).

Aby otrzymać parametryczne przedstawienie aste-roidy, skorzystamy z tego, że jak wynika z jej równania, suma kwadratów wyrażeń (xla)¹¹³ i (yla)^u3 jest równa jedności. Przyjmując, że wyrażenia te są równe cos t i sin t, otrzymujemy następujące równania parametryczne

x — acos¹t,    y = asin¹f    (0<f<2n).

Ponieważ obie pochodne

x',— —3a cos² / sin t,. yl=3a sin²1 cos/

są równe zeru, gdy t=0 (2n), |n, n, |7t, przeto tym wartościom parametru odpowiadają punkty osobliwe; są to te same punkty co wyżej.

5) Liść Kartezjusza (rys. 117):

x¹+y¹-laxy=0(^l)    (a> 0).

Punktem osobliwym jest początek układu (0, 0); w punkcie tym krzywa sama siebie przecina. Dla jc-* + oo i dla — co krzywa ma asymptotę o równaniu ^+y + a = 0. Aby się o tym przekonać, podzielmy równanie obustronnie przez x¹:

=3a -

Stąd przede wszystkim można wywnioskować, że powiedzmy dla |x|>3a iloraz \ylx\ jest ograniczony. Z tego zaś wynika, że gdy x-3±ao, to y/x-t — 1. Z drugiej strony, z równania krzywej otrzymujemy

3 a-

'-HtF

y+x=

a więc dla x~* ± °o suma y+x~*—a. Zatem rzeczywiście prosta x+y+a — 0 jest asymptotą [148], Wprowadzając jako parametr stosunek t=y/x i podstawiając w równaniu krzywej y—tx, otrzymujemy przedstawienie parametryczne liścia Kartezjusza

3 at

3al²

/¹ + l

t¹ +1

(—oo<t< + co;/^—1).

(') Patrz np. 2) ustęp 210. Punkt A (a \/2, a\/Ą) odpowiadający maksimum y jako funkcji x zaznaczony jest na rysunku.

1

axy

x²-xy+y²