0509

510

VII. Zastosowania rachunku różniczkowego do geometrii

Korzystając ze wzorów na krzywiznę wyprowadzonych w poprzednim ustępie, możemy od razu napisać następujące wzory na promień krzywizny:

(6)

(7)

(7a)

(7b)

R =

R=

R=

ds

^R=fa'

(*;²+y;²)^3/2

x'_ty'_ti-x;iy_t'

(l + y'_x^zf¹²

y**

(r² + r'_e²)³¹² r²+2r'_e² — rr'_a'x

Wzory te stosuje się odpowiednio do sposobu przedstawienia krzywej.

Z wszystkich tych wzorów promień krzywizny — podobnie jak wyżej krzywiznę -otrzymujemy ze znakiem. Jednak teraz nie będziemy znaku odrzucali, lecz postaramy się wyjaśnić jego znaczenie geometryczne.

W tym celu wprowadzimy zwrot dodatni na normalnej do krzywej. Wyjaśniliśmy już w ustępie 249, że na stycznej jako dodatni przyjmujemy zwrot w stronę wzrastania luku. Na normalnej zaś jako dodatni przyjmujemy taki zwrot, aby skierowana styczna i skierowana normalna tworzyły parę o orientacji zgodnej z orientacją pary osi x i y układu współrzędnych. Np. przy zwykłym położeniu osi układu normalna powinna powstawać ze stycznej przez obrót o kąt +\n w kierunku przeciwnym do ruchu wskazówki zegara.

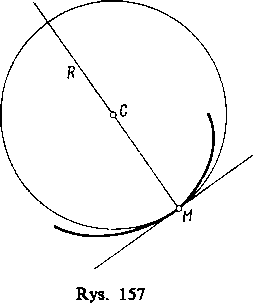
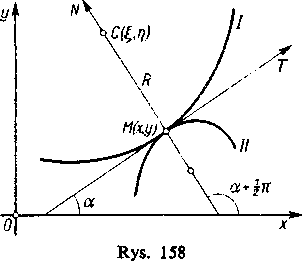
Teraz rozpatrujemy promień krzywizny R=MC jako odcinek skierowany, leżący na normalnej, i naturalnie przypisujemy mu znak plus, gdy jest on skierowany zgodnie z dodatnim zwrotem normalnej i znak minus w przeciwnym wypadku. Tak więc na rysunku 158 w przypadku krzywej I promień krzywizny jest dodatni, a w przypadku krzywej II ujemny.

Twierdzimy, że znak promienia krzywizny otrzymany z któregokolwiek z wyprowadzonych wyżej wzorów ściśle odpowiada podanej przed chwilą definicji. Trzeba jednak