0455

456

VII. Zastosowania rachunku różniczkowego do geometrii

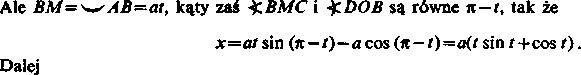
y — CM—CF+FM=DB+FM—

=OB sin %.DOB+BMcos BMC — a (sin t—t cos t). Tak więc ewolwenta może być przedstawiona równa

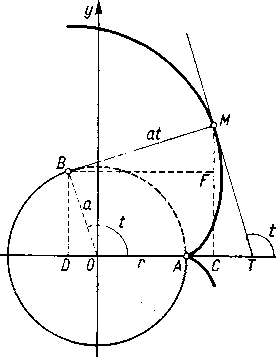
x

Rys. 121

niami parametrycznymi

ją a (/sin f+cos /),    j> = a(sin/ —/cos/).

Jedyny punkt osobliwy odpowiada wartości t = 0, dla której są równe zeru obie pochodne

x‘, — at cos I,    y', = atsint.

Proponujemy czytelnikowi przekonać się, że otrzymuje się tę samą krzywą, jeśli się toczy bez ślizgania prostą po kole i rozpatruje trajektorię dowolnego punktu tej prostej.

226. Krzywe na płaszczyźnie we współrzędnych biegunowych. Przykłady. Często okazuje się,

że prościej jest przedstawić krzywą równaniami biegunowymi, ustalającymi zależność między współrzędnymi biegunowymi r, 9 punktu krzywej. Kąt biegunowy 9 mierzymy od osi biegunowej, przy tym jest on dodatni, gdy powstaje przez obrót w kierunku przeciwnym do ruchu wskazówek zegara. Biegunowy promień wodzący r może być dodatni i ujemny, w pierwszym przypadku odkładamy go w kierunku określonym przez kąt 9, a w drugim — odkładamy go na tej samej prostej, lecz w przeciwną stronę.

Podobnie jak w przypadku współrzędnych prostokątnych zależność r oA 9 może być dana w postaci nieuwikłanej, uwikłanej lub parametrycznej. Ograniczymy się głównie do najprostszego przypadku, gdy krzywa jest przedstawiona równaniem nieuwikłanym postaci r=f{9).

Jeżeli przejdziemy do współrzędnych prostokątnych przyjmując, jak się to zwykle robi, biegun za początek układu i oś biegunową za oś jc, to równania

x = r costf=/(0) cos0, y = r sin9—f(9) sin0

są parametrycznym przedstawieniem tej krzywej, przy czym rolę parametru gra kąt 9. Otrzymane w ten sposób funkcje zmiennej 9 są wraz z funkcją / ciągłe i mają ciągłe pochodne, bo własność tę z założenia ma funkcja /.

Wzory

Xg = r'_e cos 9 — r sin 9, y'e = r'₉ sin0 + r cosó

pokazują, że punkt osobliwy (w sensie określonym w ustępie 223) może się zdarzyć tylko wtedy, gdy r = r'_e-0.