051

51

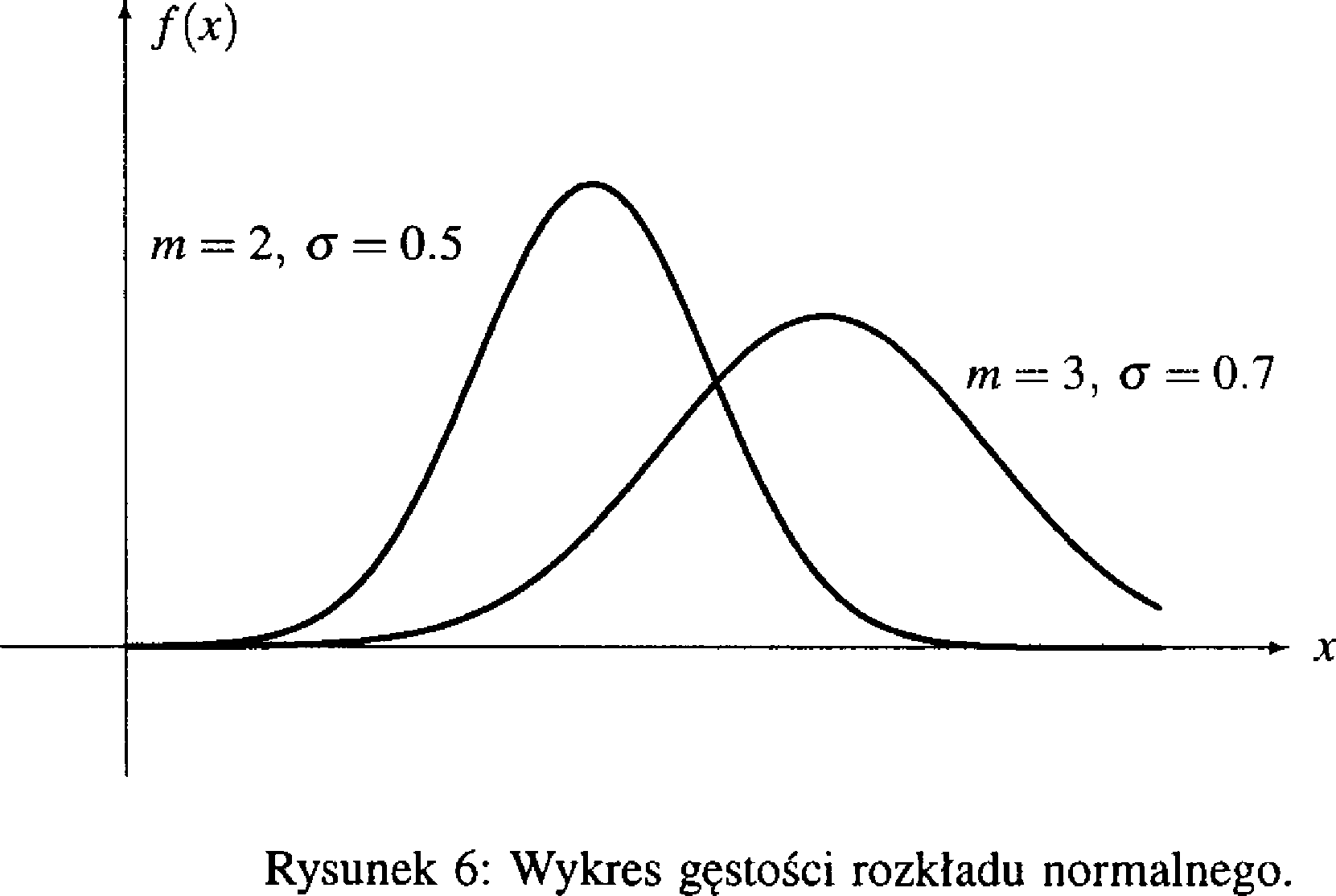
2.4. Rozkłady ciągłe

korzystać z programów komputerowych. (Patrz procedura normOl .pas). Bez żadnych obliczeń mamy jednak 4>(0) = 0.5.

Ze względu na wzór (2.4.7), wartości dystrybuanty rozkładu N(m,a) można otrzymać z wartości dystrybuanty rozkładu N(0,1). Czasem w tablicach zamiast wartości dystrybuanty <£(*) podaje się wartości funkcji

*»^w=7b/'"’^/2‘"-

0

Dla x > 0 zachodzi oczywisty związek 3>(jc) = <£₀(jc) +0.5 oraz *(-*) = 0,5 — <t>₀(;c). Ponieważ <$₀(0) —0, to mając dane tablice, łatwo można się zorientować po wartości w zerze, czy stablicowana jest funkcja <E>(jc) czy %(x). W skrypcie tym podana jest tablica wartości dystrybuanty 3>(jc).

W dalszym ciągu będziemy wielokrotnie korzystali z poniższego wyniku, którego dowód pozostawimy do paragrafu 2.5 jako zadanie 2.5.6.

Twierdzenie 2.4.2.

Jeślo X_x, X₂, • -., X_n są niezależnymi zmiennymi losowymi o rozkładach

N^-, O)), to, że X_x +X₂ -I-----\-X_n ma rozkład N(m, a), gdzie m = m_x +m₂ +

—h m_n oraz cr = of + a\ H-----h <7^.

Rąuła

3-sigmowa

Rozkład normalny ma następującą własność, znaną jako reguła 3-sigmowa. Fakt 2.4.1.

Jeżeli zmienna losowa X ma rozkład normalny N(m, o), to

(2.4.10)

Pr(|X — m| > 3cr) < 0.01.