058

58

2. Zmienne losowe

Momenty

Twierdzenie 2.5.3.

Istnienie k-tego momentu zmiennej losowej jest równoważne istnieniu k-tej pochodnej jej funkcji charakterystycznej, przy czym

i^k

Bezpośrednio ze wzoru (2.5.1) wynika wzór, analogiczny do znanych wzorów w przekształceniu Laplace’ a:

(p(t) dla rozkładu wykładniczego

<P_ax(‘) = <Px(^at)-

Z kolei z twierdzenia 2,5.2 wynika, że

gdyż stałą a można traktować jako zmienną losową przyjmującą tylko jedną wartość a, a taka zmienna losowa jest niezależna od dowolnych zmiennych losowych i ma funkcję charakterystyczną (co łatwo sprawdzić) równą e^lła.

Wyznaczymy teraz funkcje charakterystyczne rozkładów typu ciągłego, które były przedstawione w paragrafie 2.4. Obliczenie funkcji charakterystycznej rozkładu jednostajnego pozostawimy jako zadania 2.5.1 i 2.5.2, wyznaczymy natomiast funkcje charakterystyczne rozkładu wykładniczego i normalnego.

Przykład. Dla rozkładu wykładniczego z parametrem X funkcję charakterystyczną obliczamy ze wzoru (2.5.1). Mamy

co

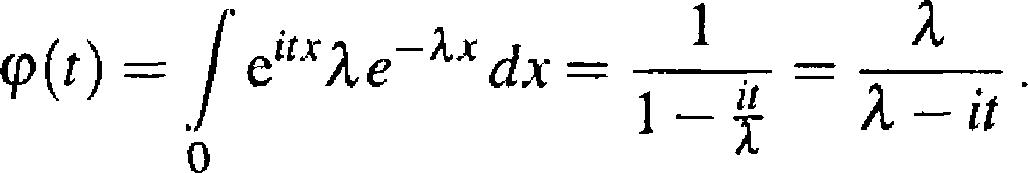
(2.5.2)

(p(t) dla rozkładu normalnego

Przykład. Dla rozkładu normalnego:

oo

ę(t) — —)= I Q~(^x~^lt^/²e~^t2/²dx — e~*²/², V27r J

— oo

gdyż

oo

1

V)²/2 j i

— OO