16 M3 KobierskiM SzypowskaK ZAD164

18,4 ■ X₂ — —5,55 ■ q ■ a

X₂

37

120

■ q ■ a

X₁ = 0,425 ■ q ■ a — 0,6 ■    ■ q ■ a — 0,61 ■ q ■ a

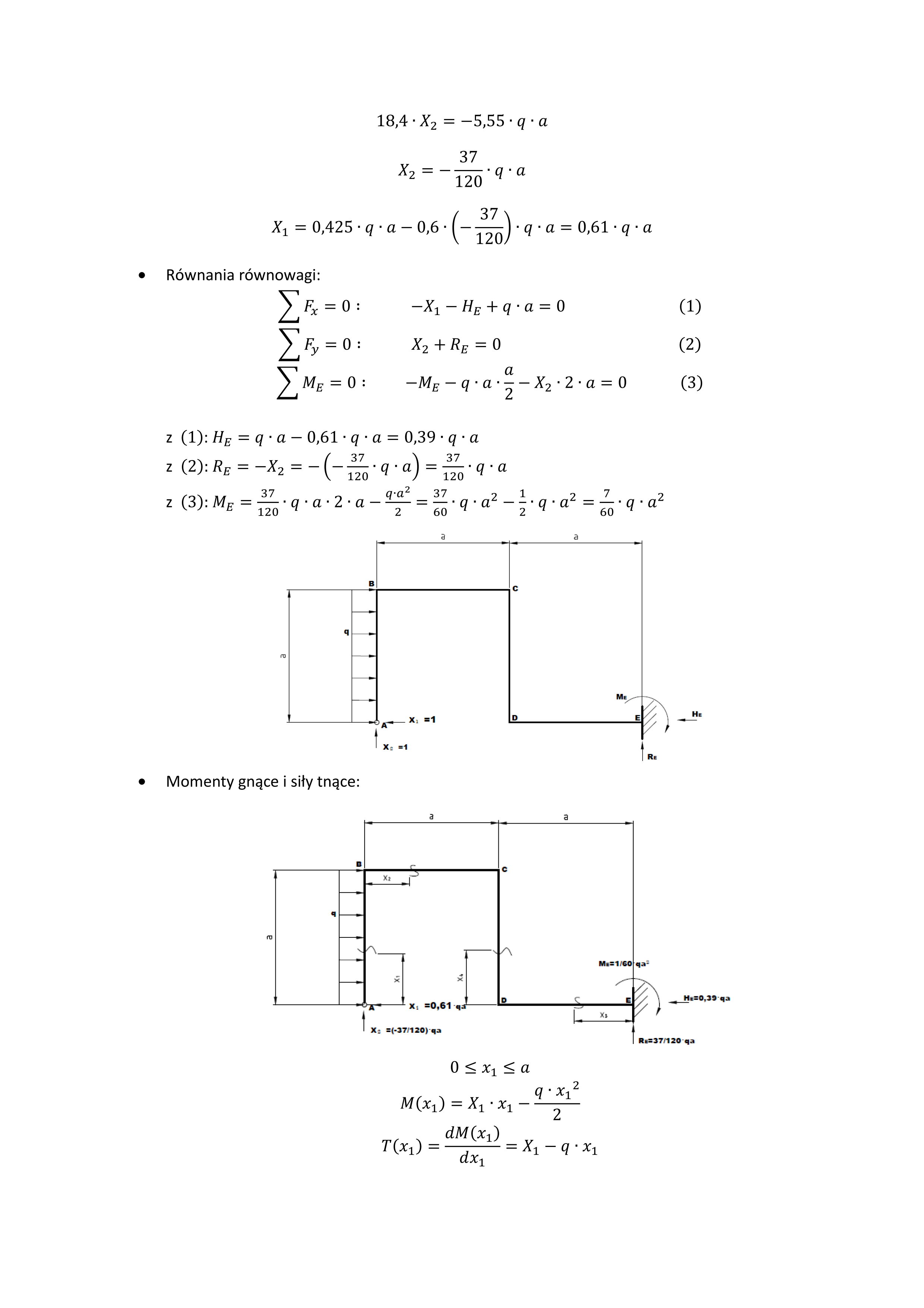
• Równania równowagi:

5>-	0 :	—X1 — HE + q ■ a = 0	(1)
II w	0 :	X2 3" Re ^= 0	(2)
V^1		a
1^M^1 =	: 0 :	—Me — q ■ a ■ — — X2 ■ 2 ■ a — 0	(3)

z (1): H_e = q ■ a — 0,61 ■ q ■ a = 0,39 ■ q ■ a z (2):R_E = -X₂ = -(-^-_o-q-a) = ^-_o-q-a

n/i 37    ₀    cfa² 37    2    1    2    ⁷

^v ' ^c 120 ^ 2 60 ^ 2 ⁿ 60

0 <    < a

,    ,    1' ^xi²

M(x₁)=X₁-x₁-^~ cLM(xi)

^TOi) = _d =X₁-q-x₁

1

Momenty gnące i sity tnące: