1 (176)

fi ■ K X Q    M - (u.Vtlluji3_ /KJ^^ŚoO, ^

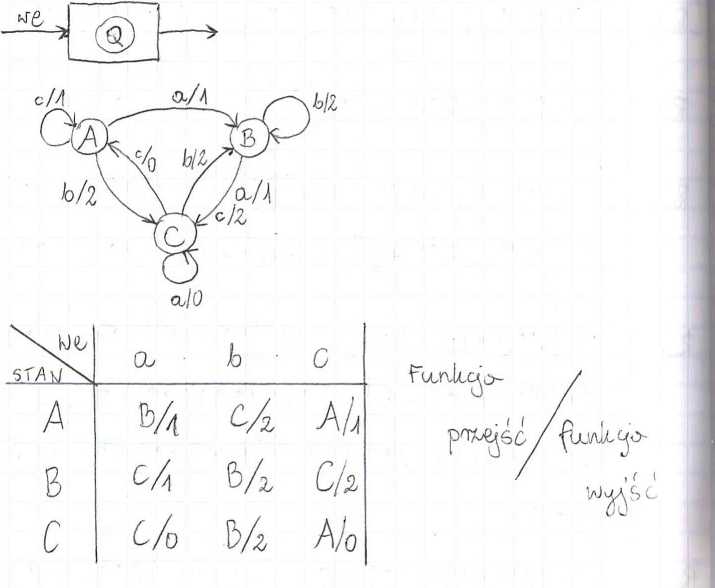
l[A$ ⁼ c*[ab* (a⁺c) + b^T_c0

^-Ąc * Ia^

^Ł

•co

To *⁺<X⁴ O

t cc

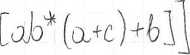
(cL+c) Cjo A/g

WYHtAD 9

Def.

/\ lUto Roi,e,VK ę,k>o^cuyyjĄ yw S^^CWv M -i^d^Cg.;

*■ l V l Q , $ ' ^ uj Ojujto^fyyo^cx£, M oo^ lx-- Q/"łto + bTgiO + cTmj + a + 6

^d°T_n

(VU3- WV U

Tao ~ 0/ 'co + to^T&o+cXto ł/\0 ~    lo Mo ⁺ C' ' AO

jLtOal&j    ^oJc ur cuAcmćUic Moovc’cu

l’Jp ⁼ b* \Ou+l) Tco

Tlo - CbTco ⁴ b b* (o^^c)~to + cTao +cl^ ■1>0 ^ i2,b*ftL⁺c)TGo + b\oo + _LcTĄO

V-

■Tco * aJcg⁴ i)t* (&+k)Jęo,+ cc*[ab*(<l<-c) łb]jcu> r_co:~ oo ⁺ bb^ł (cl/^+c) + cc^oJo* [iO^c

T_co* bb* (<x+c)

c-> c

Auiwmai hofiCTjj ui luifttam-    oui

stawte 0. ^{15    3}    ^