5125715749

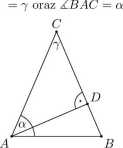
Rozwiązanie. Oznaczmy ZACB

Wtedy 7 = 180° — 2a, czyli a = ¹⁸⁰2 7 = 90° — Stąd dostajemy

AB AD = a - AC AD = a - (90° - 7) = 90° - | - 90° +7 = |, czyli ZACB = 7 = 2 • /.BAD.

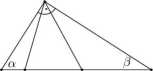
3. Na przeciwprostokątnej AB trójkąta prostokątnego ABC wybrano punkty D i E w taki sposób, by AC = AE oraz BC = BD. Udowodnij, że /DCE = 45°. Rozwiązanie. Oznaczmy kąty ostre trójkąta ABC tak jak na rysunku:

C

A D E    B

Ponieważ AC = AE, więc /ACE = /AEC = ¹⁸⁰° ^Q = 90° — Stąd wynika, że /BCE = W podobny sposób pokazujemy, że /ACD = Zatem

/DCE = 90°

a

2

a + /3 2

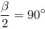
90°

90°

2

45°.

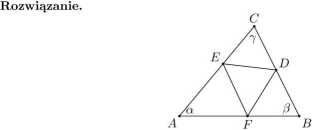
4. Dany jest trójkąt ABC, w którym /BAC = o, /ABC = (3 oraz /ACB = 7. Na bokach BC, AC i .AE tego trójkąta wybrano odpowiednio punkty D, E 1 F w taki sposób, by AE = AE, BD = RE i CE = CE. Udowodnij, że

7

2'

ZEEE =    = 90°

7