109 2

216 X. Badanie przebiegu zmienności funkcji

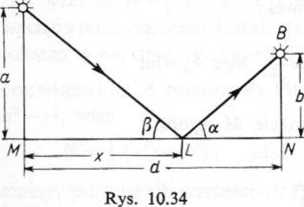
Rozwiązanie. Oznaczmy AL + LB = 5; stosując twierdzenie Pitagorasa otrzyj

jemy	<5 = 's/ci^2 -\-x^1 b^2 ~\~(d — x)^2.
Obliczamy pochodną	dó x d—x
	d* \la^2+x^2 \/b^2+(d — x)^2

Przyrównując pochodną do zera otrzymujemy

x    d — x

y/a²+x²    'Jb²+(d-x)²

gdzie, jak wiemy,

= cos /?.

— cos a,

+ X

d — x

sj b² +(d — x)

Wykazaliśmy więc, że a = fi.

A

B

Rys. 10.35

Zadanie 10.41. Znane jest prawo załamania światła przy przejściu z jednego ośrodka do drugiego:

(1)    sin ę>i_Vi

sin <p₂ v₂

gdzie <Pi oznacza kąt padania światła (czyli kąt między promieniami światła i normalną do powierzchni oddzielającej ośrodki), <p₂ — kąt załamania (również względem normalnej), a Dj i v₂ są to prędkości rozchodzenia się światła w danych ośrodkach (rys. 10.35)-Wykazać, że powyższy wzór można wyprowadzić z następującej zasady:

Jeżeli promień światła przebiega z punktu A w jednym ośrodku do punktu B w dru gim ośrodku, przy czym prędkości rozchodzenia się światła w tych ośrodkach są różn^e* to promień wybiera taką drogę, żeby czas przebiegu z punktu A do punktu B był możli'^vie najmniejszy.

Rozwiązanie. Przypuśćmy, że promień wychodzący z punktu A przebija płaszczy®^ rozdzielającą ośrodki w punkcie C i po załamaniu dochodzi do punktu B. Z zasady ¹⁽¹¹⁰¹

alnego czasu wynika, że każdy z odcinków AC i CB musi być prostoliniowy, ponieważ ⁿ' _każdym z ośrodków prędkość jest stała.

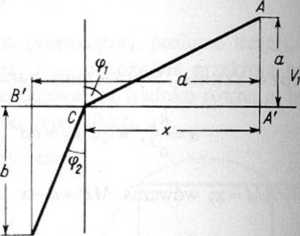
" Niechaj A' i B' oznaczają rzuty punktów A i B na płaszczyznę rozdzielającą ośrodki, p_{rzeZ rz}uty ,4' i B' przechodzi płaszczyzna prostopadła do płaszczyzny rozdzielającej ,_srodki. Punkt załamania C musi leżeć w tej płaszczyźnie na linii prostej A'B', gdyż jeżeliby _unkt C nie leżał na prostej A'B’, to jego rzut C' na tę prostą dawałby w każdym ośrodku jjótszą drogę (gdyż AC'<AC i BC'<BC). Widzimy więc, że punkty A i B oraz normalna ,₀ płaszczyzny rozdzielającej ośrodki w punkcie załamania C leżą w jednej płaszczyźnie. Rysunek 10.35 przedstawia tę płaszczyznę.

Wprowadźmy oznaczenia AA'—a, BB' = b, A'B' = d i A'C=x. Obliczamy

AC=\Ja² +x²,    BC=s/b²+(d-x)².

Czas t przebiegu drogi od A do C i od C do B wyraża się wzorem

\la²+x² \lb² +(d—x)²

t=-+ ----

t>i    v₂

Trzeba znaleźć taką wartość x, dla której czas t jest najmniejszy.

Wyznaczymy teraz najkrótszy czas przebycia drogi od A do B. Obliczmy pochodną

dt    x    d—x

dx Uj y/a²+x² v₂ \/b²+(d- x)² Pochodna dtjdx przybiera wartość 0, gdy

x    d—x

... -    : ■ .    - =v_t:v₂,

Vn²+x² \/b²+(d—x)²

a ponieważ x[\!a² + x² = sin cp^, (d—x)]\lb² + (d—x)² = sm <p₂, więc

sin cp_x v_t sin (p₂ v₂

Udowodniliśmy więc, że z prawa o przebywaniu drogi przez promień świetlny w minimalnym czasie wynika wzór (1).

Zadanie 10.42. Puszka do konserw w postaci walca o pojemności 547tma być tak wy-°^nana, by została zużyta minimalna ilość blachy (minimum powierzchni). Wyznaczyć Pfomień r podstawy i wysokość h puszki.

Rozwiązanie. Objętość puszki Trr²/z = 547i; stąd

*-n.

r

^°le powierzchni puszki obliczone według wzoru S=2nr² + 2nrh wynosi

,    108 n

S=2nr²+-•

(1)