039 2

Badanie przebiegu zmienności funkcji

3. Parzystość i nieparzystość funkcji

/(*) =

x — 1

x² + 3.v - 4

/(-*) =

-x- 1 X² - 3x - 4

~f(x) =

x² + 3x — 4

X + 1

x² + 3x - 4

=>/(■'-') *f{~x) oraz /(- x) * -f(x)

Funkcja nie jest parzysta, jak również nie jest nieparzysta.

4. Granice

lim f(x) = lim

x-»-oc    ,v—> ~

x- I

x² + 3x - 4 x 1

oo ”

„00

Ponieważ przy x-> -os uzyskujemy symbol nieoznaczony, dzielimy licznik i mianownik przez najwyższą potęgę mianownika.

lim /(x) = -

x

X

3x

.0

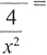
= lim

,v—»—co

I

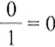
lim f(x) = lim

x->+oc    x-»+ao

1

x² + 3x - 4

oo ”

„00

Postępujemy analogicznie jak w przypadku, gdy

x-+ +30.

= lim -

X—> 4- =0

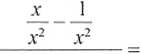
3x 4

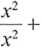
1

= lim

X—> 4-30

1

0

1

= 0

y = O asymptota pozioma obustronna.

Badanie przebiegu zmienności funkcji

X - 1

lim f(x) = lim . -r—--j

.v->-4    ,v-»-4 A + 3x ~~ 4

Rysujemy wykres znaku mianownika, czyli: sgn (x + 4).

= lim

: lim

-i—>-■ 4 (X +    *-»-4 A + 4

lim /(a) = lim    7————7 =

,v-> 4⁺-^{/ v} ’    .v~>~4⁺ X² + 3a - 4

1

= lim . -———xi = lirm-;

•t->-4 (a 4- 4^0 .v->-4 X + 4

.A''^T

O

lim /(a) = lim

a-> 1    .v—> 1

lim, /(a) = lim

lim =

ć + 3x- 4 = (x + 4)(x- 1) zgodnie ze wzorem ał + bx + c - a{x- xj(x- x₁), gdy A > 0, a * 0.

= + oc

x = - 4 asymptota pionowa obustronna.

1 1 1

“ r (a + 4 )(a?—T5    r _x + 4 1+4 5

,.111

: lim -    “    ^_

.<->r ' ' '    x->i*(x + 4)Qt^łJ .v->i⁺ a + 4    1-4 5

W tym przypadku nie ma asymptoty pionowej w punkcie a = 1.

Asymptota ukośna

y = ax + h, gdy

f(x)

a = lim ——, b = lim (/(a) - ax)

.Y—> ± CC X    ,V-> ± 3C

A - 1

/(a)    a²+3a-4

a = lim --= lim -= lim

a- 1

.V—> ± co    X    .V—>± »

= lim

A- 1

lim

a    ,x->=-/.a'(a² + 3a - 4)

A___1_

A³    A³

Mii a³ + 3a² - 4a .v-4±» a³ ^ 3a²    4a

1 / 1

A^J A

= lim

A'->±00

A" A^J

1 +

V

_3    4

A    A²

o o*

b = lim (/(a) - ci(a)) = lim

a² + 3x - 4

- 0 • a = lim

a- 1

Asymptota ta ma równanie y = 0.

77