036

Badanie przebiegu zmienności funkcji

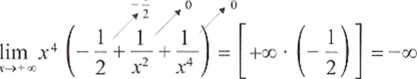
czyli

lim f(x) = -oo

Brak asymptot poziomych.

Asymptota pionowa nie istnieje, ponieważ z dziedziny żaden punkt nie został usunięty.

Asymptota ukośna

Równanie asymptoty ukośnej ma postać: y = ax + b, gdzie

a - lim    b = lim (f(x) - ax)

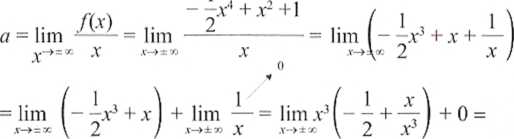
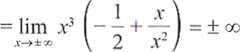
Zatem a nie istnieje.

Wobec tego b też (wynika to ze wzoru na b). Brak asymptoty ukośnej.

5. Pochodna

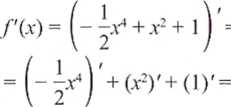
- • f, ■ a^j+ 2 ■ X¹ + O =

l

Korzystamy ze wzoru na pochodną sumy funkcji oraz na pochodną funkcji (Z")'= w V"^-1

2x³ + 2.v

6-7. Monotoniczność i ekstrema funkcji

f'(x) = - 2x³ + 2x, D = R W.K

f'(x) = 0 o - 2x³ + 2x = 0 x(- 2x² + 2) = 0 x = 0 lub - 2x² + 2 = 0 /:2 x ⁼ 0 lub x² = 1 x = 0, x= 1, x = -l,

max min max

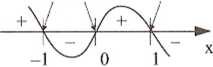
Rysujemy wykres znaku pochodnej. sgn/'(x) = sgn(- 2x² + 2) x e (-oo; -1) =>/(x) /i x e (-1; 0) =>/(x) \j x € (0; 1) =>/(x) / x e (1; +oo) =>/(x)\j

.U- 0=^

X,J0)=1

,    1

/ (1)= 1 —

•Mim' ⁷    2

8. Tabelka przebiegu zmienności funkcji

x e	(-00,-1)	-1	(-1,0)	0	(0,1)	-1	(l,+oo)
/'(X)	+	0	-	0	+	0	-
/(X)		max		min		max	>

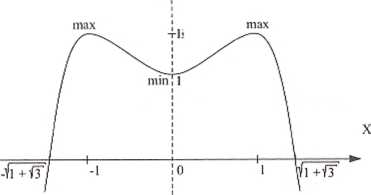
9. Wykres

Yi

71