095 2

188 X. Badanie przebiegu zmienności funkcji

§ 10.4. WYPUKŁOŚĆ 1 WKLĘSŁOŚĆ FUNKCJI

Niech będą dane dwie liczby <x₂. Wypukłą kombinacją (por. str. 149) tych itfg, nazywamy każdą liczbę postaci

(10.4.1)    x_a=ax_l+(\-a)x₂, gdzie 0<a«$l .

Czytelnik łatwo udowodni, że każda liczba postaci (10.4.1) spełnia nierówność

(10.4.2)

to znaczy, że każda wypukła kombinacja dwóch liczb leży na odcinku, którego końcami sj te liczby.

Mówimy, że funkcja /(x) określona w przedziale <Z>, c> jest wypukła w tym przedział jeżeli dla każdej liczby postaci (10.4.1) przy dowolnych Xi i x₂ z przedziału <ń, _c> _2a. chodzi nierówność

(10.4.3)    f(.x_a)^y„, gdzie y_a=af(x_l)+(l-a)f(x₂).

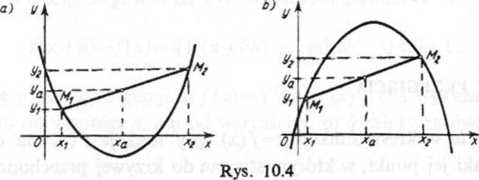
Na podstawie geometrii analitycznej wiemy, że punkt (x_a, y_a), gdzie x₀ określone wzorem (10.4.1), a y_a wzorem (10.4.3), leży na odcinku, którego końcami są punkty o współrzędnych M_i(x₁,y_i) i M₂(x₂ , y₂) ■ Warunek (10.4.3) wypukłości funkcji f(x) oznacza więc geometrycznie, że luk wykresu funkcji y=f(x) o końcach M₁ i M₂ znajduje się całkowicie poniżej cięciwy M₂M₂, jakiekolwiek obierzemy punkty ńij i M₂ wykresu funkcji wypukłej (rys. 10.4a).

Zachodzą następujące twierdzenia:

(10.4.4)    Jeżeli funkcja f (x) jest w przedziale (b, c) róźniczkowałna, a jej pochodna fi' w tym przedziale funkcją rosnącą, to funkcja f (x) jest w przedziale <ń, c> funkcją wy pakt

(10.4.5)    Jeżeli funkcja f(x) jest w przedziale <b,c> dwukrotnie róźniczkowałna, a druga pochodna przyjmuje w tym przedziale stale wartości dodatnie, to funkcja /(*) w przedziale (b, c) funkcją wypukłą.

Aby udowodnić (10.4.4) wystarczy zauważyć, że nierówność (10.4.3) jest równoważ nierówności

f(x_a)~f(xi) J(x₂)-f(x_a)

(10.4.6)

X_a X±    X2 x_a

która, jeżeli do obu stron zastosujemy wzór Lagrange’a, wynika z założenia, że p°^c f’(x) jest funkcją rosnącą.    &

Twierdzenie (10.4.5) wynika z twierdzenia (10.4.4), ponieważ na podstawie

twierdzenia Lagrange'a, jeżeli druga pochodna /"(x) jest w pewnym przedziale stale ^jjjtnia, to pierwsza pochodna f'(x) jest w tym przedziale funkcją rosnącą.

tyłowi my, że funkcja f(x) określona w przedziale <6, c> jest wklęsła w tym przedziale, _cżelj dla każdej liczby postaci (10.4.1) przy dowolnych i x₂ z przedziału <c, d} ^chodzi nierówność

(10.4.7)    f(x„)>y., gdzie y_a=af(x_l)+(l-a)f(x₂).

Jeżeli funkcja jest wklęsła, to łuk wykresu funkcji znajduje się zawsze ponad cięciwą, łączącą końce luku (rys. 10.4b).

Jeżeli funkcja f(x) posiada w przedziale <c, d) pierwszą pochodną malejącą lub drugą pochodną ujemną, to jest w tym przedziale funkcją wklęsłą.

Można wykazać, że jeżeli funkcja f (x) jest w przedziale (b, c> wypukła (wklęsła) i dwukrotnie róźniczkowałna, to w każdym punkcie wykresu funkcji styczna do wykresu znajduje się pod (nad) wykresem (patrz rys. 10.5).

Przy podanych definicjach wypukłości i wklęsłości kształty wykresu odpowiadają naszemu wyobrażeniu wypukłości i wklęsłości, jeżeli patrzymy na wykres z kierunku, odpowiadającego ujemnemu zwrotowi osi rzędnych.

o

x

0

Rys. 10.5

Zadanie 10.8. Zbadać przebieg zmienności trójmianu kwadratowego y = ax² + bx+c.

Rozwiązanie. Obliczmy pochodne y' = 2ax + b, y" = 2a. Widzimy, że y=0, gdy ^x=~b/2a. Wtedy mamy

b 2 a

y = a —2~b— +c = 4 a

Aac — b²

Aa

A

Aa ’

Udzie A—b² — Aac (wyróżnik trójmianu kwadratowego).

Pochodna y" ma natomiast stały znak — taki, jak znak współczynnika a. Rozróź-^IUamy więc dwa przypadki:

Przypadek 1: a>0. Wówczas tabelka przebiegu zmienności trójmianu ma postać

X	— OO		b la		+ 00
y"	+ 00	+	+	+	+ 00
y	— 00	-	0	+	+ 00
y	+ 00		_Ą_ 4a		+ oo