045 2

Badanie przebiegu zmienności funkcji

Asymptota ukośna

f(x) ~X^ "ł" 2 A'² y = ax + b, gdzie a = lim = lim---= lim (-a³ + 2x) ■

X~>±cc X    -V—>±oo    A    A‘—>± oc-

= lim

X—>=oc

a nie istnieje b również nie istnieje

^; ioo

Asymptoty ukośnej nie ma.

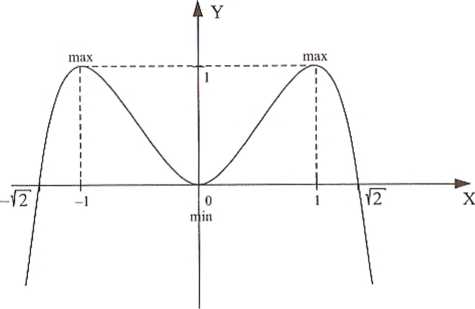
5. Pochodna

/'(*) = (-a⁴ + 2a²)' = (-.v⁴)' + (2 a²)' = = - 4x³ + 4a

6-7. Monotoniczność i ekstrema funkcji

f'(x) = ~4xⁱ + 4x W.K

f'(x) = O o -4a³ + 4a = O

4a(- a² + 1) = O x = O lub x² - 1 x = O, x= 1, a — 1 sgn f'(x) = sgn (-4„v³ + 4.v)

X e (-oo;-1) =>f(x)7'

xe (-1; O)=>/(*) \i

x e (0; l)=>/(x)/i

x 6 (1; +=o) => f(x) \

Korzystamy ze wzoru (a •**)' = a •*•**•’

max min max

Badanie przebiegu zmienności funkcji

8. Tabelka

x e	(-00;-i)	-1	(-1; 0)	0	(0; 1)	1	(l;+co)
m	+	0	-	0	4-	0	-
m		max		min		max

89